ясность, так как мы cделаем это профессией
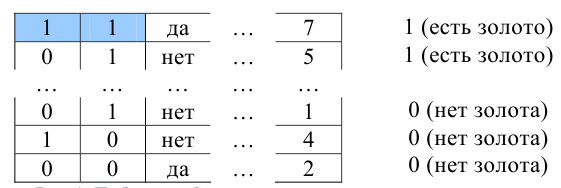
В 60-х годах прошлого века, как тогда говорили, «партия и правительство» (а точнее Председатель Совета Министров СССР Косыгин Алексей Николаевичએ) поручили геологам найти на территории СССР месторождение золота африканского типа. Всего таких месторождений в мире было семь, они представляют собой «золотые блины» толщиной 10–15 сантиметров на глубине 2–3 километра (т.е. найти их «случайно» почти невозможно). Имелась полная статистика по ним: пробы грунта, снимки местности и т.д. Имелась также статистика по местам, в которых специалисты предполагали наличие золота, но тщательный анализ установил его отсутствие. Такую статистику в анализе данных часто собирают в таблицы «объект-признак», пример показан на рис. 1: по строкам записаны описания месторождений (объектов), а столбцы соответствуют некоторым признакам (мнение одного эксперта, особенность рельефа и т.д.).
Для консультации два молодых геолога (А.Н. Дмитриев и Ф.П. Кренделев) обратились в Институт математики новосибирского Академгородка. Проблемой заинтересовался математик Журавлёв Юрий Ивановичએ. На вид это была как раз математическая задача: интерполяция функции от многих переменных (функция равна единице на описаниях месторождений золота и нулю – на описаниях остальных мест, надо определить, где она ещё будет равна единице, кроме известных семи точек). Проблема была только в том, что переменных больше сотни, а точек, в которых известны значения функции, всего несколько. Задача казалась неразрешимой, по крайней мере, методами «классической математики», но помог случай. За год до этого Академгородок посетил американский профессор Э. Фейгенбаум, который в своих лекциях утверждал, в частности, что ни одна по-настоящему сложная задача не может быть решена чисто математическим путём, необходимо использовать человеческий опыт, «подсматривать», как решают задачу специалисты и разрабатывать эвристические алгоритмы. Ю.И. Журавлёв ухватился за эту идею, долго беседовал с геологами, выяснял, как вообще принято искать полезные ископаемые, и переводил эти «геологические» идеи в математическую форму.
В результате был изобретён алгоритм для поиска золота. С точки зрения «чистой математики» он был некорректен (сама постановка задачи была не совсем корректна), но он сработал! Описывать алгоритм в этой лекции мы не будем, но объясним один из основных принципов его работы. Рассмотрим рис. 1. Если подописание (1,1) (выделено в таблице) встречается только в первых двух признаках объектов первого класса и не встречается в объектах второго класса, то наличие такого подописания характерно для объектов первого класса. Это называют элементарным тестовым классификатором, их строят много, причём строят так, чтобы они были «неупрощаемы», т.е., например, если сократить это подописание, то значение 1 в первом признаке (или во втором) уже не будет характерно ни для одного из классов. Для нового объекта (потенциального месторождения), который надо классифицировать, смотрят, какие классификаторы «голосуют» за его вхождение в первый класс, а какие – за вхождение во второй. В простейшем случае «прислушиваются к большинству».
Описание алгоритма Косыгин Алексей Николаевичએ выслушал лично, а ведущий кибернетик того времени, академик Глушков Виктор Михайловичએ назвал этот алгоритм «шаманским», что было справедливо: «математическим» его можно было назвать с натяжкой. Так появился этот термин. На самом деле, события, описанные выше, являются началом целого направления научных исследований.
Впервые эта история была рассказана в научно-популярной лекции «ШАМАНСТВО» В АНАЛИЗЕ ДАННЫХ доцента ВМК МГУ имени М.В. Ломоносова, д.ф.-м.н. А.Г. Дьяконова
