Описательная статистика на Python (часть 1)

В эпоху больших данных и искусственного интеллекта Data Science^એ и Machine Learning^એ стали обязательным элементом многих областей науки и техники. При этом одним из важнейших аспектом работы с данными являются возможности их описания, обобщения и визуального представления. Библиотеки статистики Python — это комплексные, популярные и широко используемые инструменты, которые помогают работать с цифрами.

В этой статье вы узнаете:

• какие числовые величины можно использовать для описания и обобщения ваших наборов данных;
• как вычислить описательную статистику на Python;
• с помощью каких доступных библиотек Python можно получить описательную статистику;
• как визуализировать ваши наборы данных.

Понятие описательной статистики

Описательная статистика — это описание и интегральные параметры наборов данных. Она использует два основных подхода:

1. Количественный подход, который описывает общие численные характеристики данных.
2. Визуальный подход, который иллюстрирует данные с помощью диаграмм, графиков, гистограмм и прочих графических образов.

Описательную статистику можно применять к одному или нескольким наборам данных или переменных. Когда вы описываете и вычисляете характеристики одной переменной, то выполняете одномерный анализ. Когда вы ищете статистические связи между парой переменных, то вы делаете двухмерный анализ. Аналогичным образом, многомерный анализ связан с несколькими переменными одновременно.

Виды метрик

Здесь вы узнаете о следующих метриках описательной статистики:

1. Центральные метрики, которые говорят вам о центрах концентрации данных, таких как среднее^એ, медиана^એ и мода^એ.
2. Метрики оценки вариативности данных, которые говорят о разбросе значений, такие как дисперсия^એ и стандартное отклонение^એ.
3. Метрики оценки корреляции или взаимозависимости, которые указывает на связь между парой переменных в наборе данных, такие как ковариация^એ и коэффициент корреляции^એ.

Вы узнаете, как понимать и вычислять эти меры с помощью Python.

Наблюдения и выборки

Наблюдения или генеральная совокупность^એ в статистике — это набор всех элементов, относительно которых предполагается делать выводы при изучении конкретной задачи. Зачастую генеральная совокупность очень велика, что делает её непригодной для сбора и анализа. Вот почему в статистике обычно пытаются сделать некоторые выводы о популяции, выбирая и исследуя репрезентативную подгруппу этой совокупности.

Такое подмножество называется выборкой. В идеале выборка должна удовлетворительно сохранять существенные статистические характеристики генеральной совокупности. Таким образом, можно использовать выборку для получения выводов о наблюдениях.

Выбросы

Выброс — это такая точка, которая существенно отличается от большинства значений, взятых из выборки или совокупности. Есть множество возможных причин появления выбросов и вот для начала только несколько:

1. Естественные выбросы данных.
2. Изменение поведения наблюдаемой системы.
3. Ошибки при сборе данных.

Наиболее частой причиной появления выбросов являются Ошибки сбора данных. Например, ограничения измерительных приборов или самих процедур сбора информации и это означает, что правильные данные просто не могут быть получены. Другие ошибки могут быть вызваны просчетами, зашумлением данных, человеческой ошибкой и многое-многое другое.

Точного математического определения выбросов не существует. И здесь необходимо полагаться на собственный опыт, знания о предмете интереса и здравый смысл, чтобы понять, действительно ли подозрительная точка является аномалией в данных и как следует с ней обращаться.

Выбор библиотек статистики Python

Существует множество библиотек статистики Python, с которыми можно работать, но здесь мы рассмотрим только некоторых из них, самые популярные и широко используемые:

1. Python statistics — встроенная библиотека Python для описательной статистики. Вы можете использовать её, если ваши наборы данных не слишком велики или если вы не можете полагаться на импорт других библиотек.
2. NumPy^એ — сторонняя библиотека для численных вычислений, оптимизированная для работы с одномерными и многомерными массивами. Его основным типом является тип массива называется ndarray. Эта библиотека содержит множество подпрограмм для статистического анализа.
3. SciPy^એ — сторонняя библиотека для научных вычислений, основанная на NumPy^એ. Она предлагает дополнительную функциональность по сравнению с NumPy, в том числе scipy.stats для статистического анализа.
4. Pandas^એ — сторонняя библиотека для численных вычислений, основанная на NumPy. Она отлично справляется с обработкой помеченных одномерных (1D) данных с объектами Series и двумерных (2D) данными объектами DataFrame.
5. Matplotlib^એ — сторонняя библиотека для визуализации данных. Он хорошо работает в сочетании с NumPy, SciPy и Pandas.
6. plotly — сторонняя библиотека для визуализации данных, самая продвинутая на сегодняшний день. Она позволяет создавать интерактивные динамические истории для глубокого погружения в данные и хорошо работает в сочетании с NumPy, SciPy и Pandas.

Обратите внимание, что во многих случаях Series DataFrame вместо массивов NumPy можно использоваться и объекты. Часто вы можете просто передать их в статистическую функцию NumPy или SciPy. Кроме того, из объектом Series или DataFrame вы можете получить немаркированные данные такие, как объект np.ndarray, вызвав методы .values или .to_numpy().

Начало работы с библиотеками статистики Python

Встроенная библиотека Python statistics имеет относительно небольшое количество наиболее важных статистических функций. Официальная документация является ценным ресурсом для уточнения нюансов. Если вы ограничены чистым Python, то statistics Python может быть правильным выбором.

Хорошее место для начала изучения numpy^એ — это официальное руководство пользователя, особенно разделы быстрый старт и основы. Справочное руководство освежит вашу память по конкретным вопросам NumPy. Убедиться в мощности и полезности Numpy можно прочитав статью «Нескучный Numpy». Во время чтения полезно будет подглядывать официальную справку scipy.stats.

Примечание:

При изучении NumPy ознакомьтесь с этими ресурсами:

• Глянь Ма, никаких циклов: работа с массивами, используя NumPy
• Pythonic Data Cleaning With Pandas and NumPy
• NumPy arange(): How to Use np.arange()

Если вы хотите изучать Pandas, то официальная страница «Getting Started» — то самое место, с которого надо начать. Введение в структуры данных позволит вам узнать об основных типах данных Series и DataFrame. Кроме того, отличная официальная 10‑минутка 10 minutes to pandas придаст импульс для эффективного использования Pandas на практике.

Примечание:

При изучении Pandas ознакомьтесь с этими ресурсами:

• Pandas DataFrames 101
• Idiomatic Pandas: Tricks & Features You May Not Know
• Fast, Flexible, Easy and Intuitive: How to Speed Up Your Pandas Projects

Для matplotlib есть полное официальное руководство пользователя, где есть все детали использования библиотеки. Анатомия Matplotlib является отличным ресурсом для начинающих, которые хотят начать работать с этой библиотекой.

Примечание:

Для более полного знакомства с визуализацией ознакомьтесь с этими ресурсами:

• Python Plotting With Matplotlib (Guide)
• Python Histogram Plotting: NumPy, Matplotlib, Pandas & Seaborn
• Interactive Data Visualization in Python With Bokeh
• Dash — передовой web‑фреймворк Python

Расчет описательной статистики

Далее при чтении рекомендую использовать простейший инструмент для работы IDLE, который устанавливается автоматом при скачивании Python c python.org позволяет работать в режиме интерактивного интерпретатора. Только не забудьте установить требуемые пакеты. Эти строчки необходимо набрать в командной строке cmd:

# для начала перейдите в папку, где у вас установлен Python
cd python path 

# а теперь в командной строке можно выполнить:
pip install numpy
pip install scipy
pip install pandas
pip install matplotlib

Начните с импорта в свои скрипты всех пакетов, которые нам понадобятся:

import math
import statistics
import numpy as np
import scipy.stats
import pandas as pd

Это все пакеты Python, которые вам пока потребуются для расчетов описательной статистики. Обычно вы не будете использовать math, встроенный в Python, но здесь это будет полезно. Позже вы будете импортировать matplotlib.pyplot для визуализации данных.

Давайте создадим некоторые исходные данные. Мы начнём со списков Python, содержащих произвольные числовые данные:

>>> x = [8.0, 1, 2.5, 4, 28.0]
>>> x_with_nan = [8.0, 1, 2.5, math.nan, 4, 28.0]
>>> x
[8.0, 1, 2.5, 4, 28.0]
>>> x_with_nan
[8.0, 1, 2.5, nan, 4, 28.0]

Теперь у вас есть списки x и x_with_nan. Они почти одинаковы, с той разницей, что x_with_nan содержат nan значение. Важно понимать поведение процедур статистики Python, когда они сталкиваются с не-числовым значением (nan). В науке о данных пропущенные значения являются общими и вы часто будете заменять их на nan.

Примечание:

Как получить значение nan?

В Python можно использовать:

• float(‘nan’)
• math.nan
• np.nan

>>> math.isnan(np.nan), np.isnan(math.nan)
(True, True)
>>> math.isnan(y_with_nan[3]), np.isnan(y_with_nan[3])
(True, True)

Практически, всё это одно и то же. Однако, надо помнить, что результатом сравнения двух значений nan будет False. Значение выражения math.nan == math.nan есть False!

Теперь создайте объекты np.ndarray и pd.Series, соответствующие x и x_with_nan:

>>> y, y_with_nan = np.array(x), np.array(x_with_nan)
>>> z, z_with_nan = pd.Series(x), pd.Series(x_with_nan)
>>> y
array([ 8. ,  1. ,  2.5, 4. , 28. ])
>>> y_with_nan
array([ 8. ,  1. ,  2.5,  nan,  4. , 28. ])
>>> z
0     8.0
1     1.0
2     2.5
3     4.0
4    28.0
dtype: float64
>>> z_with_nan
0     8.0
1     1.0
2     2.5
3     NaN
4     4.0
5    28.0
dtype: float64

Теперь у вас есть два массива NumPy (y и y_with_nan) и два объекта Series Pandas (z и z_with_nan). Все это — 1D‑последовательности значений.

Примечание:

Хотя здесь мы используем списки, но, пожалуйста, имейте в виду, что в большинстве случаев точно так-же можно использовать кортежи.

При необходимости можно указать метку для каждого значения в z и z_with_nan.

Центральные метрики

Центральные метрики показывают центр или средние значения наборов данных. Существует несколько определений того, что считается центром набора данных. Здесь вы узнаете, как определить и рассчитать эти метрики, используя Python:

• Среднеарифметическое;
• Средневзвешенное;
• Среднегеометрическое;
• Гармоническое среднее;
• Медиана;
• Мода.

Среднее значение набора данных, среднеарифметическое, знакомо всем со школьной скамьи:

X_{average} = \frac{\sum_{i=1}^{N}(X_i)}{N}

Другими словами, это сумма всех элементов X_i, деленная на количество элементов в наборе данных.

На этом рисунке показано среднее значение выборки, которую мы определили, с пятью точками данных:

Зеленые точки представляют собой точки данных 1, 2.5, 4, 8 и 28. Красная пунктирная линия — это их среднее значение, или (1 + 2.5 + 4 + 8 + 28) / 5 = 8.7.

Вы можете вычислить среднее значение на чистом Python, используя sum() и len(), без импорта библиотек:

>>> mean_ = sum(x) / len(x)
>>> mean_
8.7

Хотя это чисто и элегантно, вы также можете применить встроенные функции статистики Python:

>>> mean_ = statistics.mean(x)
>>> mean_
8.7
>>> mean_ = statistics.fmean(x)
>>> mean_
8.7

Вы вызвали функции mean() и fmean() из встроенной библиотеки statistics Python и получили тот же результат. fmean() вводится в Python 3.8 как более быстрая альтернатива mean(). Она всегда возвращает число с плавающей запятой.

Однако если среди ваших данных есть значения nan, то statistics.mean() и statistics.fmean() вернутся nan в качестве результата:

>>> mean_ = statistics.mean(x_with_nan)
>>> mean_
nan
>>> mean_ = statistics.fmean(x_with_nan)
>>> mean_
nan

Этот результат связан с поведением sum(). Ведь sum(x_with_nan) также возвращает nan.

Если вы используете NumPy, то вы можете получить среднее значение с помощью np.mean():

>>> mean_ = np.mean(y)
>>> mean_
8.7

В приведенном выше примере, mean() это функция, но можно использовать соответствующий метод .mean():

>>> y.mean()
8.7

И функция, и метод ведут себя аналогично при наличии значений nan среди ваших данных:

>>> np.mean(y_with_nan)
nan
>>> y_with_nan.mean()
nan

Вам часто не нужно получать учитывать nan в результате. Если вы предпочитаете игнорировать nan, то вы можете использовать np.nanmean():

>>> np.nanmean(y_with_nan)
8.7

nanmean() просто игнорирует все значения nan и возвращает то же самое значение, что mean() если из набора данных удалить все значения nan.

Объекты pd.Series также имеют метод .mean():

>>> mean_ = z.mean()
>>> mean_
8.7

Как вы можете видеть, он используется так же, как и в случае NumPy. Однако .mean() Pandas игнорирует значения nan по умолчанию:

>>> z_with_nan.mean()
8.7

Это поведение является результатом назначения необязательного параметра skipna по умолчанию. Этот параметре можно изменить.

Средневзвешенное

Средневзвешенное или также называемое средневзвешенным арифметическим или средневзвешенным значением, является обобщением среднего арифметического, которое позволяет вам определить относительный вклад каждой точки данных в результат.

Вы определяете один вес w_i для каждой точки данных x_i набора данных x, где = 1, 2,…, n и n — количество элементов в x. Затем вы умножаете каждую точку данных на соответствующий вес, суммируете все произведения и делите полученную сумму на сумму весов:

\frac{\sum_{i=1}^{N}(w_i * x_i)}{\sum_{i=1}^{N}w_i}

Примечание

Обычно, все веса неотрицательны, w_i >= 0 и их подбирают так, что сумма равна единице или {\sum_{i=1}^{N}w_i} = 1.

Средневзвешенное значение очень удобно, когда вам нужно среднее значение набора данных, содержащего элементы, которые встречаются с заданными относительными частотами. Например, допустим, что у вас есть набор, в котором 20% всех элементов равны 2, 50% элементов равны 4, а оставшиеся 30% элементов равны 8. Вы можете вычислить среднее значение такой набор, как это:

>>> 0.2 * 2 + 0.5 * 4 + 0.3 * 8
4.8

Здесь вы учитываете частоты с весами. При использовании этого метода вам не нужно знать общее количество элементов.

В чистом Python средневзвешенное можно реализовать комбинацией sum() с range() или zip():

>>> x = [8.0, 1, 2.5, 4, 28.0]
>>> w = [0.1, 0.2, 0.3, 0.25, 0.15]
>>> wmean = sum(w[i] * x[i] for i in range(len(x))) / sum(w)
>>> wmean
6.95
>>> wmean = sum(x_ * w_ for (x_, w_) in zip(x, w)) / sum(w)
>>> wmean
6.95

Опять же, это чистая и элегантная реализация, в которой вам не нужно импортировать какие-либо библиотеки.

Однако, если у вас большие наборы данных, то NumPy, вероятно, будет лучшим решением. Вы можете использовать np.average() для массивов NumPy или серии Pandas:

>>> x = [8.0, 1, 2.5, 4, 28.0]
>>> y, z, w = np.array(x), pd.Series(x), np.array(w)
>>> wmean = np.average(y, weights=w)
>>> wmean
6.95
>>> wmean = np.average(z, weights=w)
>>> wmean
6.95

Результат такой же, как и в случае чистой реализации Python. Этот метод можно использовать для обычных списков и кортежей.

Кроме того, можно использовать поэлементное умножение w * y с np.sum() или .sum():

>>> (w * y).sum() / w.sum()
6.95

Это оно! Вы рассчитали средневзвешенное значение.

Однако, будьте осторожны, если ваш набор данных содержит значения nan:

>>> w = np.array([0.1, 0.2, 0.3, 0.0, 0.2, 0.1])
>>> (w * y_with_nan).sum() / w.sum()
nan
>>> np.average(y_with_nan, weights=w)
nan
>>> np.average(z_with_nan, weights=w)
nan

В этом случае average() возвращает nan в связи с алгоритмом np.mean().

Гармоническое среднее

Гармоническое среднее есть обратная величина от среднего значения обратных величин всех элементов в наборе данных:

\frac{n}{\sum_{i=1}^{n}(\frac{1}{x_i})},

где i = 1, 2,…, n и n — количество элементов в наборе данных . Один из вариантов реализации гармонического среднего на чистом Python:

>>> hmean = len(x) / sum(1 / item for item in x)
>>> hmean
2.7613412228796843

Он сильно отличается от значения среднего арифметического для тех же данных x, которые мы рассчитали ранее 8,7.

Вы также можете рассчитать эту меру с помощью statistics.harmonic_mean():

>>> hmean = statistics.harmonic_mean(x)
>>> hmean
2.7613412228796843

В приведенном выше примере показана одна из реализаций statistics.harmonic_mean(). Если в наборе данных есть значение nan, оно вернет nan. Если хотя бы один 0, то он вернет 0. Если вы укажете хотя бы одно отрицательное число, вы получите статистику StatisticsError:

>>> statistics.harmonic_mean(x_with_nan)
nan
>>> statistics.harmonic_mean([1, 0, 2])
0
>>> statistics.harmonic_mean([1, 2, -2])  # Raises StatisticsError

Помните об этом при использовании этого метода!

Третий способ вычисления среднего значения гармоники — использовать scipy.stats.hmean():

>>> scipy.stats.hmean(y)
2.7613412228796843
>>> scipy.stats.hmean(z)
2.7613412228796843

Это, Опять же, довольно простая реализация. Однако, если ваш набор данных содержит nan, 0, отрицательное число или что-то кроме положительных чисел, то вы получите ValueError!

Среднее геометрическое

Среднее геометрическое является корнем n-степени произведения всех элементов x_i в наборе данных x:

\sqrt[n]{(\prod_{i}x_i)},

где i = 1, 2,…, n. На следующем рисунке показаны средние арифметические, гармонические и геометрические значения набора данных:

Снова, зеленые точки — точки данных 1, 2.5, 4, 8 и 28. Красная пунктирная линия — среднее арифметическое. Синяя пунктирная линия — гармоническое среднее, а желтая пунктирная линия — геометрическое среднее.

На чистом Python вычисление геометрического среднего можно реализовать следующим образом:

>>> gmean = 1
>>> for item in x:
...     gmean *= item
...
>>> gmean **= 1 / len(x)
>>> gmean
4.677885674856041

Как видите, для одного и того же набора данных x значение геометрического среднего значительно отличается от значений среднего арифметического (8,7) и гармонического (2,76)

Начиная с Python 3.8 введен statistics.geometric_mean(), который преобразует все значения в числа с плавающей точкой и возвращает их среднее геометрическое значение:

>>> gmean = statistics.geometric_mean(x)
>>> gmean
4.67788567485604

Вы получили тот же результат, что и в предыдущем примере, но с минимальной ошибкой округления.

Если вы передадите данные со значениями nan, то statistics.geometric_mean() будет вести себя как большинство похожих функций и вернет nan:

>>> gmean = statistics.geometric_mean(x_with_nan)
>>> gmean
nan

Действительно, это согласуется с поведением statistics.mean(), statistics.fmean() и statistics.harmonic_mean(). Если среди ваших данных есть ноль или отрицательное число, то statistics.geometric_mean() вызовет statistics.StatisticsError.

Вы также можете получить среднее геометрическое с помощью scipy.stats.gmean():

>>> scipy.stats.gmean(y)
4.67788567485604
>>> scipy.stats.gmean(z)
4.67788567485604

Вы получили тот же результат, что и в реализации на чистом Python.

Если у вас есть значения nan в наборе данных, то gmean() вернет nan. Если хотя бы один 0, он вернет 0.0 и выдаст предупреждение. Если вы укажете хотя бы одно отрицательное число, вы получите Nan и предупреждение.

Медиана

Медиана — это средний элемент отсортированного набора данных. Набор данных может быть отсортирован по возрастанию или убыванию. Если число элементов набора данных нечетное, то медиана является значением в средней позиции: 0,5( + 1). Если чётно, то медиана — это среднее арифметическое двух значений в середине, то есть элементов в позициях 0.5 и 0.5 + 1.

Например, если у вас есть точки данных 2, 4, 1, 8 и 9, то медианное значение равно 4, что находится в середине отсортированного набора данных (1, 2, 4, 8, 9). Если точками данных являются 2, 4, 1 и 8, то медиана равна 3, что является средним значением двух средних элементов отсортированной последовательности (2 и 4). Посмотрите на рисунок ниже:

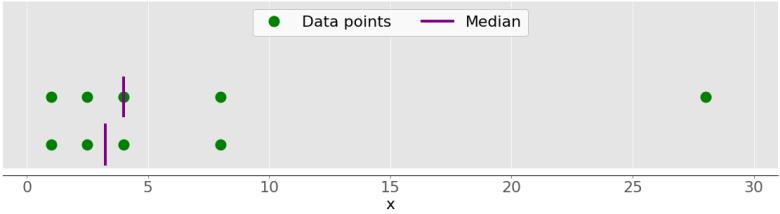
Точками данных являются зеленые точки, а фиолетовые линии показывают медиану для каждого набора данных. Медианное значение для верхнего набора данных (1, 2,5, 4, 8 и 28) равно 4. Если вы удалите выброс 28 из нижнего набора данных, медиана станет средним арифметическим между 2,5 и 4, что составляет 3,25.

На рисунке ниже показано среднее и среднее значение точек данных 1, 2.5, 4, 8 и 28:

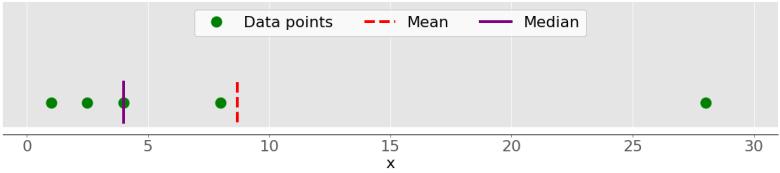
Опять же, среднее значение — это красная пунктирная линия, а медиана — фиолетовая линия.

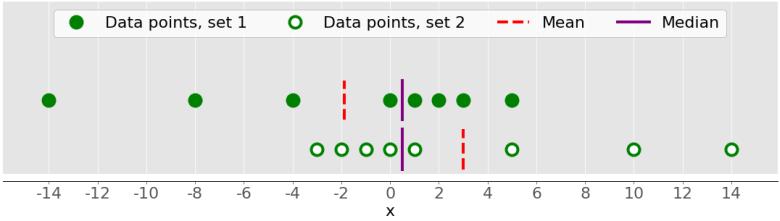
Основное различие между поведением среднего значения и медианы связано с выбросами или экстремальными значениями. Среднее значение сильно зависит от выбросов, а медиана либо незначительно зависит от выбросов, либо вообще не зависит. Посмотрим следующий рисунок:

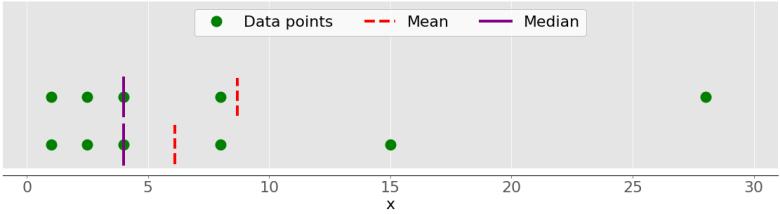
В верхнем наборе данных снова есть элементы 1, 2.5, 4, 8 и 28. Его среднее значение равно 8,7, а медиана равна 5, как вы видели ранее. Нижний набор данных показывает, что происходит, когда вы перемещаете крайнюю правую точку со значением 28:

• Если вы увеличите его значение (переместите его вправо), то среднее значение возрастет, но медианное значение никогда не изменится.
• Если вы уменьшите его значение (переместите его влево), то среднее значение уменьшится, но медиана останется неизменной, пока значение движущейся точки не станет больше или равно 4.

Вы можете сравнить среднее значение и медиану как один из способов обнаружения выбросов и асимметрии в ваших данных. Является ли среднее значение или среднее значение более полезным для вас, зависит от контекста вашей конкретной проблемы.

Вот одна из многих возможных реализаций чистого медиана Python:

>>> n = len(x)
>>> if n % 2:
...     median_ = sorted(x)[round(0.5*(n-1))]
... else:
...     x_ord, index = sorted(x), round(0.5 * n)
...     median_ = 0.5 * (x_ord[index-1] + x_ord[index])
...
>>> median_
4

Два наиболее важных шага этой реализации заключаются в следующем:

1. Сортировка элементов набора данных;
2. Нахождение средних элементов в отсортированном наборе данных.

Вы можете получить медиану с помощью statistics.median():

>>> median_ = statistics.median(x)
>>> median_
4
>>> median_ = statistics.median(x[:-1])
>>> median_
3.25

Сортированный датасет x имеет вид [1, 2.5, 4, 8.0, 28.0], поэтому элемент в середине равен 4. Сортированный датасет x[: - 1], то есть x без последнего элемента 28.0, равна [1 2,5, 4, 8,0]. Теперь есть два средних элемента, 2,5 и 4. Их среднее значение составляет 3,25.

median_low() и median_high() — еще две функции, связанные с медианой в статистической библиотеке Python. Они всегда возвращают элемент из набора данных:

• Если число элементов нечетное, то имеется одно среднее значение, поэтому эти функции ведут себя как median().
• Если число элементов четное, то есть два средних значения. В этом случае median_low() возвращает меньшее, а median_high() — большее среднее значение.

Вы можете использовать эти функции так же, как и median():

>>> statistics.median_low(x[:-1])
2.5
>>> statistics.median_high(x[:-1])
4

Опять же, отсортированный x[:-1] это [1, 2.5, 4, 8.0]. Два элемента в середине: 2,5 (низкий) и 4 (высокий).

В отличие от большинства других функций из библиотеки статистики Python, median(), median_low() и median_high() не возвращают nan при наличии значений nan среди точек данных:

>>> statistics.median(x_with_nan)
6.0
>>> statistics.median_low(x_with_nan)
4
>>> statistics.median_high(x_with_nan)
8.0

Остерегайтесь этого, может быть это не то, что вы хотите!

Вы также можете получить медиану с помощью np.median():

>>> median_ = np.median(y)
>>> median_
4.0
>>> median_ = np.median(y[:-1])
>>> median_
3.25

Вы получили те же значения с помощью statistics.median() и np.median().

Однако, если в вашем наборе данных есть значение nan, тогда np.median() выдает RuntimeWarning и возвращает nan. Если это не то, что нужно, то можно использовать nanmedian(), чтобы игнорировать все значения nan:

>>> np.nanmedian(y_with_nan)
4.0
>>> np.nanmedian(y_with_nan[:-1])
3.25

Полученные результаты такие же, как и для statistics.median() и np.median(), примененных к наборам данных x и y.

Объекты серии Pandas имеют метод .median(), который по умолчанию игнорирует значения nan:

>>> z.median()
4.0
>>> z_with_nan.median()
4.0

Поведение .median() аналогично .mean() в Pandas. Вы можете изменить это поведение с помощью необязательного параметра skipna.

Мода

Мода — это значение в наборе данных, которое встречается чаще всего. Если такого значения не существует, набор является мультимодальным, поскольку он имеет несколько модальных значений. Например, в наборе, который содержит точки 2, 3, 2, 8 и 12, число 2 является модой, потому что встречаеся дважды, в отличие от других элементов, которые встречаются только один раз.

Вот как вы можете получить режим с чистым Python:

>>> u = [2, 3, 2, 8, 12]
>>> mode_ = max((u.count(item), item) for item in set(u))[1]
>>> mode_
2

Вы используете u.count(), чтобы получить количество вхождений каждого элемента в u. Элемент с максимальным количеством вхождений — это мода. Обратите внимание, что вам не нужно использовать set(u). Вместо этого вы можете заменить его просто на u и повторить весь список.

Примечание:

set(u) возвращает набор Python только с уникальными элементами в u. Вы можете использовать этот прием для оптимизации работы с большими данными, особенно если вы ожидаете увидеть много дубликатов.

Вы можете вычислить моду с помощью statistics.mode() и statistics.multimode():

>>> mode_ = statistics.mode(u)
>>> mode_
>>> mode_ = statistics.multimode(u)
>>> mode_
[2]

Обратите внимание, mode() вернула одно значение, а multimode() в результате вернула список. Однако, это не единственное различие между двумя функциями. Если существует более одного модального значения, то mode() вызывает StatisticsError, а multimode() возвращает список со всеми режимами:

>>> v = [12, 15, 12, 15, 21, 15, 12]
>>> statistics.mode(v)  # Raises StatisticsError
>>> statistics.multimode(v)
[12, 15]

Нужно обратить особое внимание и быть осторожным при выборе между этими двумя функциями так, как statistics.mode() и statistics.multimode() обрабатывают значения nan как обычные значения и могут возвращать nan как модальное значение:

>>> statistics.mode([2, math.nan, 2])
2
>>> statistics.multimode([2, math.nan, 2])
[2]
>>> statistics.mode([2, math.nan, 0, math.nan, 5])
nan
>>> statistics.multimode([2, math.nan, 0, math.nan, 5])
[nan]

В первом примере число 2 встречается дважды, т.е является модальным значением. Во втором примере nan — это модальное значение, поскольку оно встречается дважды, тогда как другие значения встречаются только один раз.

Примечание:

statistics.multimode() появилась только в Python 3.8.

Моду, кроме того, можно получить с помощью scipy.stats.mode():

>>> u, v = np.array(u), np.array(v)
>>> mode_ = scipy.stats.mode(u)
>>> mode_
ModeResult(mode=array([2]), count=array([2]))
>>> mode_ = scipy.stats.mode(v)
>>> mode_
ModeResult(mode=array([12]), count=array([3]))

Эта функция возвращает объект с модальным значением и количество его повторений в наборе данных. Если в наборе данных несколько модальных значений, то возвращается только наименьшее.

Вы можете получить моду и количество её вхождений в виде массивов NumPy с точечной нотацией:

>>> mode_.mode
array([12])
>>> mode_.count
array([3])

Этот код использует .mode, чтобы вернуть наименьшую моду (12) в массиве v, и .count для повторений (3). scipy.stats.mode() также гибок со значениями nan. Это позволяет вам определить желаемое поведение с помощью необязательного параметра nan_policy. Этот параметр может принимать значения ‘propagate’, ‘raise’ (an error) или ‘omit’..

Для объектов серии Pandas имеется метод .mode(), который хорошо обрабатывает мультимодальные значения и по умолчанию игнорирует значения nan:

>>> u, v, w = pd.Series(u), pd.Series(v), pd.Series([2, 2, math.nan])
>>> u.mode()
0    2
dtype: int64
>>> v.mode()
0    12
1    15
dtype: int64
>>> w.mode()
0    2.0
dtype: float64

Посмотрите, .mode() возвращает новый объект pd.Series, который содержит все модальные значения. Если вы хотите, чтобы .mode() учитывал значения nan, просто передайте необязательный аргумент dropna = False.

Метрики оценки вариативности данных

Центральных метрик недостаточно для описания данных. Практически всегда необходимы метрики оценки вариативности данных, которые количественно определяют разброс точек данных. В этом разделе вы узнаете, как определить и рассчитать следующие показатели:

• дисперсия;
• среднеквадратичное отклонение;
• смещение;
• процентили;
• диапазон;

Дисперсия

Дисперсия количественно определяет разброс данных. Численно показывает, как далеко точки данных от среднего значения. Вы можете вычислить дисперсию набора данных, как

\sigma^2 =\frac{\sum_{i}(x_i - mean())^2}{(n - 1)},

где i = 1, 2,…, n и среднее значение mean() равно среднему. Если вы хотите глубже понять, почему вы делите сумму на n — 1 вместо n, то можете поглубже погрузиться в поправку Бесселя.

На следующем рисунке показано, почему важно учитывать разницу при описании наборов данных:

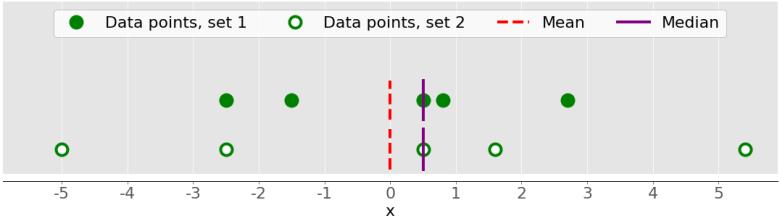
На этом рисунке представлены два набора данных:

• Зеленые точки — этот набор данных с небольшой дисперсией или небольшим отклонением от среднего. У него меньший диапазон или меньшая разница между самым большим и самым маленьким значениями.
• Белые точки — этот набор данных с большой дисперсией или большим отклонением от среднего. У него больший диапазон или большая разница между самым большим и самым маленьким значениями.

Обратите внимание, что эти два набора имеют одно и то же среднее значение и медиану, даже если они значительно различаются. Ни среднее, ни медиана не могут показать эту разницу. Вот почему нужны метрики вариативности.

Вот как вы можете рассчитать оценку дисперсии на чистом Python:

>>> n = len(x)
>>> mean_ = sum(x) / n
>>> var_ = sum((item - mean_)**2 for item in x) / (n - 1)
>>> var_
123.19999999999999

Этого достаточно и можно правильно дать оценку дисперсии. Однако, более короткое и элегантное решение — использовать функцию statistics.variance():

>>> var_ = statistics.variance(x)
>>> var_
123.2

Вы получили тот же результат для дисперсии, что и выше. Функция variance() может избежать вычисления среднего значения, если вы явно укажете среднее значение в качестве второго аргумента: statistics.variance(x, mean_).

Если среди ваших данных есть значения nan, то statistics.variance() вернет nan:

>>> statistics.variance(x_with_nan)
nan

Это связано с работой mean() и большинством других функций из библиотеки статистики Python.

Оценку дисперсии можно рассчитать, используя NumPy. Для этого необходимо использовать функцию np.var() или соответствующий метод .var():

>>> var_ = np.var(y, ddof=1)
>>> var_
123.19999999999999
>>> var_ = y.var(ddof=1)
>>> var_
123.19999999999999

Очень важно указать параметр ddof = 1, ограничивающий количество степеней свободы равными 1. Этот параметр позволяет правильно вычислять σ2, с (n - 1) в знаменателе вместо n.

Если в наборе данных есть значения nan, то np.var() и .var() вернут nan:

>>> np.var(y_with_nan, ddof=1)
nan
>>> y_with_nan.var(ddof=1)
nan

Это связано с работой функций np.mean() и np.average(). Если вы хотите пропустить значения nan, следует использовать np.nanvar ():

>>> np.nanvar(y_with_nan, ddof=1)
123.19999999999999

np.nanvar() игнорирует значения nan. Необходимо также указать ddof = 1.

Объекты pd.Series имеют метод .var(), который по умолчанию пропускает значения nan:

>>> z.var(ddof=1)
123.19999999999999
>>> z_with_nan.var(ddof=1)
123.19999999999999

Метод также имеет параметр ddof, но его значение по умолчанию равно 1, так что вы можете его опустить. Если вы хотите другое поведение, связанное со значениями nan, используйте необязательный параметр skipna.

Расчёт дисперсии генеральной совокупности производится аналогично расчёту оценки дисперсии. Однако, вы должны использовать n в знаменателе вместо n — 1:

\sigma^2 =\frac{\sum_{i}(x_i - mean())^2}{n}

В этом случае n — количество элементов всей совокупности. Вы можете получить дисперсию совокупности, аналогичную выборочной дисперсии, со следующими различиями:

• Замените (n — 1) на n в чистой реализации Python.
• Используйте statistics.pvariance () вместо statistics.variance().
• Укажите параметр ddof = 0, если вы используете NumPy или Pandas. В NumPy вы можете опустить ddof, потому что его значение по умолчанию равно 0.

Обратите внимание, что вы всегда должны знать, работаете ли вы с выборкой или со всей совокупностью при вычислении дисперсии!

Среднеквадратичное отклонение

Стандартное отклонение выборки является еще одним показателем разброса данных. Он связан с оценкой дисперсией, поскольку стандартное отклонение есть положительным квадратный корень из оценки дисперсии. Стандартное отклонение часто более удобно, чем дисперсия, потому что имеет ту же размерность, что и данные. Получив дисперсию, вы можете рассчитать стандартное отклонение с помощью чистого Python:

>>> std_ = var_ ** 0.5
>>> std_
11.099549540409285

Хотя это работает, но также можно использовать statistics.stdev():

>>> std_ = statistics.stdev(x)
>>> std_
11.099549540409287

Конечно, результат такой же, как и раньше. Как и variance(), stdev() не вычисляет среднее значение, если вы явно укажете его в качестве второго аргумента: statistics.stdev(x, mean_).

Вы можете получить стандартное отклонение с помощью NumPy практически таким же образом. Вы можете использовать функцию std() и соответствующий метод .std() для вычисления стандартного отклонения. Если в наборе данных есть значения nan, они вернут nan. Чтобы игнорировать значения nan, вы должны использовать np.nanstd(). Вы используете std(), .std() и nanstd() из NumPy точно также, как если бы вы использовали var(), .var() и nanvar():

>>> np.std(y, ddof=1)
11.099549540409285
>>> y.std(ddof=1)
11.099549540409285
>>> np.std(y_with_nan, ddof=1)
nan
>>> y_with_nan.std(ddof=1)
nan
>>> np.nanstd(y_with_nan, ddof=1)
11.099549540409285

Не забудьте установить дельта степеней свободы на 1!

Объекты pd.Series также имеют метод .std(), который по умолчанию пропускает nan:

>>> z.std(ddof=1)
11.099549540409285
>>> z_with_nan.std(ddof=1)
11.099549540409285

Параметр ddof по умолчанию равен 1, поэтому вы можете его опустить. Опять же, если вы хотите по-разному относиться к значениям nan, примените параметр skipna.

Стандартное отклонение совокупности относится ко всей совокупности. Это положительный квадратный корень дисперсии. Вы можете рассчитать его так же, как стандартное отклонение выборки, со следующими различиями:

• Найдите квадратный корень дисперсии совокупности в чистом Python.
• Используйте statistics.pstdev() вместо statistics.stdev().
• Укажите параметр ddof = 0, если вы используете NumPy или Pandas. В NumPy вы можете опустить ddof, потому что его значение по умолчанию равно 0.

Как видите, стандартное отклонение в Python, NumPy и Pandas находится практически так же, как и дисперсия. Вы используете различные, но аналогичные функции и методы с одинаковыми аргументами.

Смещение

Отклонение показывает асимметрию выборки данных.

Существует несколько математических определений асимметрии. Одним общим выражением для вычисления асимметрии набора данных x с nэлементами является

(\frac{n^2}{((n - 1) * (n - 2))}) * (\frac{\sum_i{(x_i - mean())^3}}{(n*s^3)}).

Более простым выражением является

\frac{\sum_i{(x_i - mean())^3 * n}}{(n - 1)*(n - 2) * s^3},

где n = 1, 2,…, n, а mean() — это среднее по выборке. Определенная таким образом асимметрия называется скорректированным коэффициентом стандартизированного момента Фишера-Пирсона.

На предыдущем рисунке были показаны два набора данных, которые были довольно симметричными. Другими словами, их точки были на одинаковом расстоянии от среднего. Напротив, следующее изображение иллюстрирует два асимметричных набора:

Первый набор представлен зелеными точками, а второй — белыми. Обычно отрицательные значения асимметрии указывают на то, что с левой стороны есть доминанта, которую вы видите в первом наборе. Положительные значения асимметрии соответствуют более длинному или толстому хвосту справа, который вы видите во втором наборе. Если асимметрия близка к 0 (например, между -0,5 и 0,5), то набор данных считается относительно симметричным.

После того как вы рассчитали размер набора данных n, mean_ и стандартное отклонение std_, вы можете получить асимметрию выборки с помощью чистого Python:

>>> x = [8.0, 1, 2.5, 4, 28.0]
>>> n = len(x)
>>> mean_ = sum(x) / n
>>> var_ = sum((item - mean_)**2 for item in x) / (n - 1)
>>> std_ = var_ ** 0.5
>>> skew_ = (sum((item - mean_)**3 for item in x)
...          * n / ((n - 1) * (n - 2) * std_**3))
>>> skew_
1.9470432273905929

Асимметрия положительна, поэтому у x хвост с правой стороны.

Вы также можете рассчитать асимметрию с помощью scipy.stats.skew():

>>> y, y_with_nan = np.array(x), np.array(x_with_nan)
>>> scipy.stats.skew(y, bias=False)
1.9470432273905927
>>> scipy.stats.skew(y_with_nan, bias=False)
nan

Полученный результат совпадает с реализацией на чистом Python. Для параметра «bias» установлено значение «False», чтобы включить поправки для статистического смещения. Необязательный параметр nan_policy может принимать значения 'propagate', 'raise', или 'omit'. Это позволяет вам контролировать, как вы будете обрабатывать значения Nan.

Объекты серии Pandas имеют метод .skew (), который также возвращает асимметрию набора данных:

>>> z, z_with_nan = pd.Series(x), pd.Series(x_with_nan)
>>> z.skew()м
1.9470432273905924
>>> z_with_nan.skew()
1.9470432273905924

Как и другие методы, .skew() игнорирует значения nan.

Процентили

Например, p процентиль — такой элемент в наборе данных, так что p% элементов в наборе данных меньше или равно его значению. Кроме того, (100 - p)% элементов больше или равно этому значению. Если в наборе данных есть два таких элемента, то процентиль является их средним арифметическим. Каждый набор данных имеет три квартиля, которые являются процентилями, делящими набор данных на четыре части:

• Первый квартиль — это образец 25-го процентиля. Он разделяет примерно 25% самых маленьких элементов от остальной части набора данных.
• Второй квартиль — это образец 50-го процентиля или медиана. Приблизительно 25% элементов находятся между первым и вторым квартилями и еще 25% между вторым и третьим квартилями.
• Третий квартиль — это образец 75-го процентиля. Он разделяет примерно 25% самых больших элементов от остальной части набора данных.

Каждая часть имеет примерно одинаковое количество элементов. Если вы хотите разделить ваши данные на несколько интервалов, то можно использовать statistics.quantiles():

>>> x = [-5.0, -1.1, 0.1, 2.0, 8.0, 12.8, 21.0, 25.8, 41.0]
>>> statistics.quantiles(x, n=2)
[8.0]
>>> statistics.quantiles(x, n=4, method='inclusive')
[0.1, 8.0, 21.0]

В этом примере 8,0 — медиана x, а 0,1 и 21,0 — это 25-й и 75-й процентили выборки соответственно. Параметр n определяет количество результирующих процентилей с равной вероятностью, а метод определяет, как их вычислять.

Вы также можете использовать np.percentile() для определения любого процентиля в наборе данных. Например, вот так вы можете найти 5-й и 95-й процентили:

>>> y = np.array(x)
>>> np.percentile(y, 5)
-3.44
>>> np.percentile(y, 95)
34.919999999999995

percentile() принимает несколько аргументов. Вы должны предоставить набор данных в качестве первого аргумента и значение процентиля в качестве второго. Набор данных может быть в виде массива, списка, кортежа или подобной структуры данных NumPy. Перцентиль может быть числом от 0 до 100, как в примере выше, но также может быть последовательностью чисел:

>>> np.percentile(y, [25, 50, 75])
array([ 0.1,  8. , 21. ])
>>> np.median(y)
8.0

Этот код вычисляет 25-й, 50-й и 75-й процентили одновременно. Если значение процентиля является последовательностью, то percentile() возвращает массив NumPy с результатами. Первое утверждение возвращает массив квартилей. Второе утверждение возвращает медиану, поэтому вы можете подтвердить, что она равна 50-му процентилю, то есть 8.0.

Если вы хотите игнорировать значения nan, используйте вместо этого np.nanpercentile():

>>> y_with_nan = np.insert(y, 2, np.nan)
>>> y_with_nan
array([-5. , -1.1,  nan,  0.1,  2. ,  8. , 12.8, 21. , 25.8, 41. ])
>>> np.nanpercentile(y_with_nan, [25, 50, 75])
array([ 0.1,  8. , 21. ])

Вот как можно избежать значений Nan.

NumPy также предлагает вам очень похожую функциональность в quantile () и nanquantile (). Если вы используете их, вам нужно будет указать квантильные значения в виде чисел от 0 до 1 вместо процентилей:

>>> np.quantile(y, 0.05)
-3.44
>>> np.quantile(y, 0.95)
34.919999999999995
>>> np.quantile(y, [0.25, 0.5, 0.75])
array([ 0.1,  8. , 21. ])
>>> np.nanquantile(y_with_nan, [0.25, 0.5, 0.75])
array([ 0.1,  8. , 21. ])

Результаты такие же, как в предыдущих примерах, но здесь ваши аргументы находятся между 0 и 1. Другими словами, вы передали 0.05 вместо 5 и 0.95 вместо 95.

Объекты pd.Series имеют метод .quantile():

>>> z, z_with_nan = pd.Series(y), pd.Series(y_with_nan)
>>> z.quantile(0.05)
-3.44
>>> z.quantile(0.95)
34.919999999999995
>>> z.quantile([0.25, 0.5, 0.75])
0.25     0.1
0.50     8.0
0.75    21.0
dtype: float64
>>> z_with_nan.quantile([0.25, 0.5, 0.75])
0.25     0.1
0.50     8.0
0.75    21.0
dtype: float64

Для .quantile() также необходимо указать значение квантиля в качестве аргумента. Это значение может быть числом от 0 до 1 или последовательностью чисел. В первом случае .quantile() возвращает скаляр. Во втором случае он возвращает новую серию, содержащую результаты.

Диапазон

Диапазон данных — это разница между максимальным и минимальным элементом в наборе данных. Вы можете получить его с помощью функции np.ptp():

>>> np.ptp(y)
46.0
>>> np.ptp(z)
46.0
>>> np.ptp(y_with_nan)
nan
>>> np.ptp(z_with_nan)
46.0

Эта функция возвращает nan, если в вашем массиве NumPy есть значения nan. Если вы используете объект серии Pandas, он вернет число.

В качестве альтернативы вы можете использовать встроенные функции и методы Python, NumPy или Pandas для вычисления максимумов и минимумов последовательностей:

• max() и min() из стандартной библиотеки Python;
• amax() и amin() из NumPy;
• nanmax() и nanmin() из NumPy, чтобы игнорировать значения nan;
• .max() и .min() от NumPy;
• .max() и .min() из Pandas, чтобы игнорировать значения nan по умолчанию.

Вот несколько примеров того, как вы будете использовать эти процедуры:

>>> np.amax(y) - np.amin(y)
46.0
>>> np.nanmax(y_with_nan) - np.nanmin(y_with_nan)
46.0
>>> y.max() - y.min()
46.0
>>> z.max() - z.min()
46.0
>>> z_with_nan.max() - z_with_nan.min()
46.0

Вот как вы получаете диапазон данных.

Межквартильный диапазон — это разница между первым и третьим квартилем. Как только вы вычислите квартили, вы можете взять их разницу:

>>> quartiles = np.quantile(y, [0.25, 0.75])
>>> quartiles[1] - quartiles[0]
20.9
>>> quartiles = z.quantile([0.25, 0.75])
>>> quartiles[0.75] - quartiles[0.25]
20.9

Обратите внимание, что вы получаете доступ к значениям в объекте серии Pandas с метками 0,75 и 0,25.

Сводка описательной статистики

SciPy и Pandas предлагают полезные процедуры для быстрого получения описательной статистики с помощью одного вызова функции или метода. Вы можете использовать scipy.stats.describe() следующим образом:

>>> result = scipy.stats.describe(y, ddof=1, bias=False)
>>> result
DescribeResult(nobs=9, minmax=(-5.0, 41.0), mean=11.622222222222222, variance=228.75194444444446, skewness=0.9249043136685094, kurtosis=0.14770623629658886)

В качестве первого аргумента необходимо передать набор данных, который может быть представлен массивом NumPy, списком, кортежем или любой другой подобной структурой данных. Можно опустить ddof = 1, так как это значение по умолчанию и имеет значение только при расчете дисперсии. Указано bias = False для принудительного исправления асимметрии и эксцесса статистического смещения.

description() возвращает объект, который содержит следующую описательную статистику:

• nobs — количество наблюдений или элементов в вашем наборе данных;
• minmax — кортеж с минимальными и максимальными значениями;
• mean — среднее значение;
• variance — дисперсия;
• skewness — асимметрия;
• kurtosis — эксцесс вашего набора данных.

Эти значения можно получить по отдельности:

>>> result.nobs
9
>>> result.minmax[0]  # Min
-5.0
>>> result.minmax[1]  # Max
41.0
>>> result.mean
11.622222222222222
>>> result.variance
228.75194444444446
>>> result.skewness
0.9249043136685094
>>> result.kurtosis
0.14770623629658886

В SciPy функция от описательной сводной статистики для вашего набора данных единственная.

В Pandas похожая, если не лучшая, функциональность. Объекты Series имеют метод .describe():

>>> result = z.describe()
>>> result
count     9.000000
mean     11.622222
std      15.124548
min      -5.000000
25%       0.100000
50%       8.000000
75%      21.000000
max      41.000000
dtype: float64

Если вы хотите, чтобы результирующий объект Series содержал другие процентили, то следует указать значение дополнительного параметра процентили. Вы можете получить доступ к каждому элементу результата с его меткой:

>>> result['mean']
11.622222222222222
>>> result['std']
15.12454774346805
>>> result['min']
-5.0
>>> result['max']
41.0
>>> result['25%']
0.1
>>> result['50%']
8.0
>>> result['75%']
21.0

Вот так можно получить описательную статистику объекта Series с помощью одного вызова метода с использованием Pandas.

Использованы материалы: Python Statistics Fundamentals: How to Describe Your Data