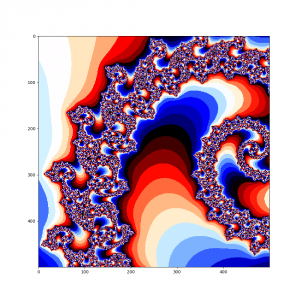
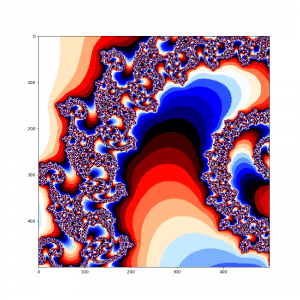
В 1985 году я прочитал статью Александра К. Дьюдни, ведущего раздел занимательной науки журнала “Scientific Americanએ”, о множестве Мандельброта, написал программу его визуализации на цветном телевизоре, подключенном через модуль крейта CAMAC к машинке MERA-CAMAC-125/СМ4А. После чего мы с коллегами могли часами генерировать и рассматривать завораживающие картинки, записывая выдающиеся в файлы на память. После упомянутой публикации подобные множества стали необычайно популярны, например, множество Мандельброта использовал в качестве своей эмблемы фонд Соросаએ. Гораздо позже, лет через десять, когда меня поразил Парадокс береговой линииએ, я узнал красивое и непонятное словосочетание «голоморфная динамика».
Голоморфная динамикаએ — область математики, где живут множество Мандельбротаએ и множество Жюлиаએ, где кроме красивых картинок есть красивые теоремы, а что самое главное, до сих пор есть неразгаданные загадки. Впрочем, я не математик и в этой области у меня самостоятельных работ нет, что, однако, не помешает вспомнить прошлое и рассказать, как строить завораживающие картинки на популярном языке Python.
Описание алгоритма
Итак, план такой. Пусть c — некоторое комплексное число. Рассмотрим последовательность чисел z0, z1, z2, … , которая строится следующим образом:
z0 = 0, zk+1 = zk2 + c, k = 0, 1, 2,…
На каждом шаге мы берём предыдущее число, возводим в квадрат и прибавляем c. В зависимости от значения c, последовательность чисел {zk} может быть ограниченной или неограниченной. При некоторых значениях она стремительно улетает в бесконечность (конечно в пределах разрядной сетки), а при некоторых тормозится. Если последовательность ограничена, мы говорим, что c принадлежит множеству Мандельброта M.
Поскольку число c комплексное, у него есть вещественная и мнимая части. Каждое комплексное число задаётся точкой декартовой плоскости: по горизонтальной координате будем откладывать вещественную часть, а по вертикальной — мнимую. Таким образом, множество M является множеством на вещественной плоскости.
Для построения графического изображения множества Мандельброта можно использовать алгоритм, называемый escape-time. Суть его такова. Всё множество полностью расположено внутри круга радиуса 2 на плоскости. Поэтому будем считать, что если для точки c последовательность итераций функции fc = z2 + c с начальным значением z = 0 после некоторого большого их числа N (скажем, 100) не вышла за пределы этого круга, то точка принадлежит множеству и красится в черный цвет. Соответственно, если на каком-то этапе, меньшем N, элемент последовательности по модулю стал больше 2, то точка множеству не принадлежит и остается белой. Таким образом, можно получить черно-белое изображение множества, которое и было получено Мандельбротом. Вот с этого мы и начнём.
Чёрно-белое множество, то которое получил Мандельброт
import numpy as np
import matplotlib.pyplot as plt
# библиотеки
# инициализиация
pmin, pmax, qmin, qmax = -2.5, 1.5, -2, 2
# пусть c = p + iq и p меняется в диапазоне от pmin до pmax,
# а q меняется в диапазоне от qmin до qmax
ppoints, qpoints = 200, 200
# число точек по горизонтали и вертикали
max_iterations = 300
# максимальное количество итераций
infinity_border = 100
# если ушли на это расстояние, считаем, что ушли на бесконечность
image = np.zeros((ppoints, qpoints))
# image — это двумерный массив, в котором будет записана наша картинка
# по умолчанию он заполнен нулями
for ip, p in enumerate(np.linspace(pmin, pmax, ppoints)):
for iq, q in enumerate(np.linspace(qmin, qmax, qpoints)):
c = p + 1j * q
# буквой j обозначается мнимая единица: чтобы Python понимал, что речь
# идёт о комплексном числе, а не о переменной j, мы пишем 1j
z = 0
for k in range(max_iterations):
z = z ** 2 + c
# Самая Главная Формула
if abs(z) > infinity_border:
# если z достаточно большое, считаем, что последовательость
# ушла на бесконечность
# или уйдёт
# можно доказать, что infinity_border можно взять равным 4
image[ip, iq] = 1
# находимся вне M: отметить точку как белую
break
plt.xticks([])
plt.yticks([])
# выключим метки на осях
plt.imshow(-image.T, cmap='Greys')
# транспонируем картинку, чтобы оси были направлены правильно
# перед image стоит знак минус, чтобы множество Мандельброта рисовалось
# чёрным цветом
plt.show()

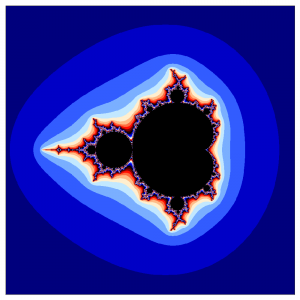
Чтобы сделать его цветным, можно, например, каждую точку не из множества красить в цвет, соответствующий номеру итерации, на котором её последовательность вышла за пределы круга.
Цветное множество, то которое за Мандельброта получили другие
import numpy as np
import matplotlib.pyplot as plt
# библиотеки
# инициализиация
pmin, pmax, qmin, qmax = -2.5, 1.5, -2, 2
# пусть c = p + iq и p меняется в диапазоне от pmin до pmax,
# а q меняется в диапазоне от qmin до qmax
ppoints, qpoints = 200, 200
# число точек по горизонтали и вертикали
max_iterations = 300
# максимальное количество итераций
infinity_border = 10
# если ушли на это расстояние, считаем, что ушли на бесконечность
def mandelbrot(pmin, pmax, ppoints, qmin, qmax, qpoints,
max_iterations=200, infinity_border=10):
image = np.zeros((ppoints, qpoints))
p, q = np.mgrid[pmin:pmax:(ppoints*1j), qmin:qmax:(qpoints*1j)]
c = p + 1j*q
z = np.zeros_like(c)
for k in range(max_iterations):
z = z**2 + c
mask = (np.abs(z) > infinity_border) & (image == 0)
image[mask] = k
z[mask] = np.nan
return -image.T
image = mandelbrot(-2.5, 1.5, 1000, -2, 2, 1000)
plt.xticks([])
plt.yticks([])
plt.imshow(image, cmap='flag', interpolation='none')
plt.show()
Изменяем палитру множества Мандельброта
import numpy as np
import matplotlib.pyplot as plt
from itertools import cycle
import matplotlib.colors as clr
# библиотеки
# инициализиация
pmin, pmax, qmin, qmax = -2.5, 1.5, -2, 2
# пусть c = p + iq и p меняется в диапазоне от pmin до pmax,
# а q меняется в диапазоне от qmin до qmax
ppoints, qpoints = 200, 200
# число точек по горизонтали и вертикали
max_iterations = 300
# максимальное количество итераций
infinity_border = 10
# если ушли на это расстояние, считаем, что ушли на бесконечность
def mandelbrot(pmin, pmax, ppoints, qmin, qmax, qpoints,
max_iterations=200, infinity_border=10):
image = np.zeros((ppoints, qpoints))
p, q = np.mgrid[pmin:pmax:(ppoints*1j), qmin:qmax:(qpoints*1j)]
c = p + 1j*q
z = np.zeros_like(c)
for k in range(max_iterations):
z = z**2 + c
mask = (np.abs(z) > infinity_border) & (image == 0)
image[mask] = k
z[mask] = np.nan
return -image.T
#image = mandelbrot(-0.793191078177363, 0.16093721735804, 1000, -0.793191, 0.160937, 1000)
plt.figure(figsize=(10, 10))
colorpoints = [(1 - (1 - q) ** 4, c) for q, c in zip(np.linspace(0, 1, 20),
cycle(['#ffff88', '#000000',
'#ffaa00', ]))]
cmap = clr.LinearSegmentedColormap.from_list('mycmap',
colorpoints, N=2048)
# LinearSegmentedColormap создаёт палитру по заданным точкам и заданным цветам
# можете попробовать выбрать другие цвета
plt.xticks([])
plt.yticks([])
image = mandelbrot(-2.5, 1.5, 1000, -2, 2, 1000)
plt.imshow(image, cmap=cmap, interpolation='none')
plt.show()

Углубляемся
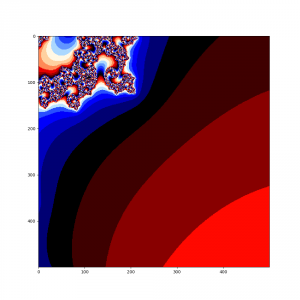
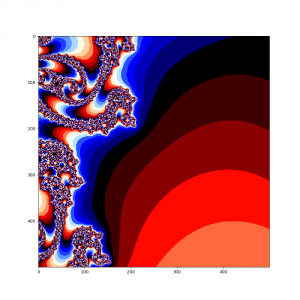
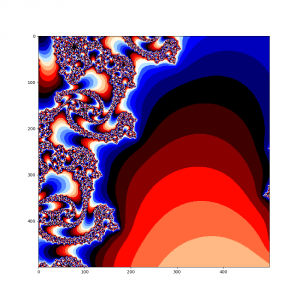
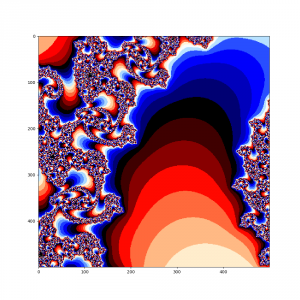
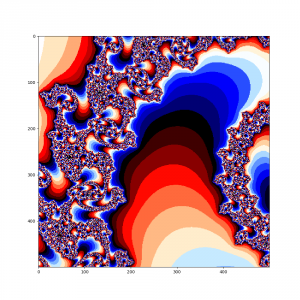
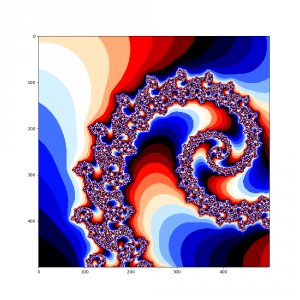
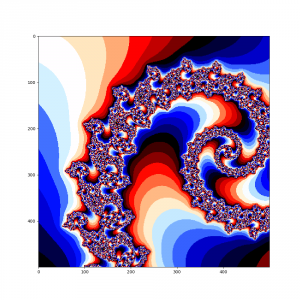
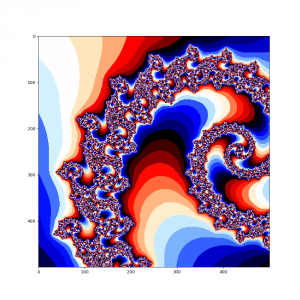
А теперь в наш алгоритм добавим еще один цикл и рассмотрим поподробнее множество Мандельброта в окрености точки -0.793191078177363, 0.16093721735804
p_center, q_center = -0.793191078177363, 0.16093721735804
for i in range(1,11):
scalefactor = i / 12000
plt.xticks([])
plt.yticks([])
pmin_ = (pmin - p_center) * scalefactor + p_center
qmin_ = (qmin - q_center) * scalefactor + q_center
pmax_ = (pmax - p_center) * scalefactor + p_center
qmax_ = (qmax - q_center) * scalefactor + q_center
image = mandelbrot(pmin_, pmax_, 500, qmin_, qmax_, 500)
print("(", pmin_, ",", pmax_, ") (", qmin_, ",", qmax_, ")")
plt.figure(figsize=(10, 10))
plt.imshow(image, cmap='flag', interpolation='none')
filename = "images//mandelbrot-" + str(i) + ".png"
plt.savefig(filename, format="png")
print(filename + " saved")
Думаю, что комментировать здесь особо нечего, итак все понятно, просто наслаждайтесь чудесами из мира фракталов.
Посмотрели. Дизайнеры, кое-что понимающие в кодировании, могут использовать приведенные алгоритмы в своем творчестве для создания оригинальных картинок и фантастических сюжетом. Все они проверены в PyCharm Community.
В качестве основы этих алгоритмов использованы коды Ильи Щурова, которые значительно переработаны и дополнены.