Содержание
Мы живем в эпоху больших данных, мощных компьютеров и искусственного интеллекта. Это только начало. Наука о данных и машинное обучениеએ стимулируют распознавание изображений, разработку автономных транспортных средств, решения в финансовом и энергетическом секторах, достижения в медицине, рост социальных сетей и многое другое. Линейная регрессия — важная часть всего этого.
Линейная регрессия — один из фундаментальных методов статистического и машинного обучения. Если вы хотите заниматься статистикой, машинным обучением или научными вычислениями, велика вероятность, что вам это понадобится. Желательно сначала изучить его, а затем переходить к более сложным методам. К концу этого урока вы узнаете:
- Что такое линейная регрессия.
- Для чего используется линейная регрессия.
- Как работает линейная регрессия.
- Как реализовать линейную регрессию в Python, шаг за шагом.
Регрессия
Регрессионный анализ — одна из важнейших областей статистики и машинного обучения. Доступно множество методов регрессии. Линейная регрессия — одна из них.
Что такое регрессия?
Регрессия ищет отношения между переменными.
Например, вы можете понаблюдать за несколькими сотрудниками какой-либо компании и попытаться понять, как их зарплата зависит от характеристик, таких как опыт, уровень образования, должность, город, в котором они работают, и т.д.
Это проблема регрессии, когда данные, относящиеся к каждому сотруднику, представляют собой одно наблюдение. Предполагается, что опыт, образование, роль и город являются независимыми характеристиками, а заработная плата зависит от них.
Аналогичным образом можно попытаться установить математическую зависимость цен на дома от их площадей, количества спален, расстояния до центра города и т.д.
Как правило, в регрессионном анализе вы обычно рассматриваете какое-либо интересное явление и получаете ряд наблюдений. Каждое наблюдение имеет две или более особенности. Исходя из предположения, что (по крайней мере) одна из характеристик зависит от других, вы пытаетесь установить связь между ними.
Другими словами, вам нужно найти функцию, которая достаточно хорошо отображает одни функции или переменные в другие.
Зависимые функции называются зависимыми переменными, выходами или откликами.
Независимые признаки называются независимыми переменными, входными данными или предикторами.
Задачи регрессии обычно имеют одну непрерывную и неограниченную зависимую переменную. Входные данные, однако, могут быть непрерывными, дискретными или даже категориальными данными, такими как пол, национальность, бренд и так далее.
Обычно выходы обозначаются y, а входы — x. Если есть две или более независимых переменных, их можно представить в виде вектора X = (x_1, \dots , x_r), где r — количество входов.
Когда вам нужна регрессия?
Регрессия, как правило, нужна для ответа на вопрос влияет ли какое-то явление на другое и как или как связаны несколько переменных. Например, вы можете использовать её, чтобы определить, влияет ли и в какой степени опыт или пол на заработную плату.
Регрессия также полезна, когда вы хотите спрогнозировать ответ, используя новый набор предикторов. Например, вы можете попытаться спрогнозировать потребление электроэнергии домохозяйством на следующий час с учетом температуры наружного воздуха, времени суток и количества жителей в этом домохозяйстве.
Регрессия используется во многих различных областях: экономике, информатике, социальных науках и так далее. Её важность возрастает с каждым днем по мере доступности больших объемов данных и повышения осведомленности о практической ценности данных.
Линейная регрессия
Линейная регрессия, вероятно, является одним из наиболее важных и широко используемых методов. Она один из самых простых методов регрессии. Одно из её главных преимуществ — простота интерпретации результатов.
Формулировка проблемы
При реализации линейной регрессии некоторой зависимой переменной y на множестве независимых переменных X = (x_1, \dots , x_r), где r — количество предикторов, вы предполагаете линейную связь между y и x:
y = \beta_0 + \beta_1x_1 + \dots + \beta_rx_r + \epsilon.
Это уравнение является уравнением регрессии. \beta_0, \beta_1, \dots , \beta_r — коэффициенты регрессии, \epsilon — случайная ошибка.
Линейная регрессия вычисляет оценки коэффициентов регрессии или просто прогнозируемых весов, обозначенных \beta_0, \beta_1, \dots , \beta_r. Они определяют оценочную функцию регрессии
f(x) = \beta_0 + \beta_1x_1 + \dots + \beta_rx_r.
Эта функция должна достаточно хорошо фиксировать зависимости между входами и выходами.
Предполагаемый или прогнозируемый ответ f(x_i) для каждого наблюдения i = 1, \dots , n должен быть как можно ближе к соответствующему фактическому значению y_i. Разности y_i - f(x_i) для всех наблюдений i = 1, \dots , n называются остатками. Регрессия — это определение наилучшего прогнозируемого веса, то есть веса, соответствующие наименьшим остаткам.
Чтобы получить наилучшие веса, вы обычно минимизируете сумму квадратов остатков (SSR) для всех наблюдений
i = 1, \dots , n: SSR = \sum_i{(y_i - f(x_i))^2}.
Такой подход называется метод наименьших квадратовએ.
Эффективность регрессии
Изменение фактических ответов y_i, i = 1, \dots , n, частично происходит из-за зависимости от предикторов x_i. Однако существует также дополнительная внутренняя дисперсия выпуска.
Коэффициент детерминации, обозначенный как R^2, сообщает вам, какое количество вариаций можно объяснить зависимостью от x с использованием конкретной регрессионной модели. Большой R^2 указывает на лучшее соответствие и означает, что модель может лучше объяснить вариации выходных данных с разными входными данными.
Значение R^2 = 1 соответствует SSR = 0, это идеальное совпадение, поскольку значения предсказанных и фактических ответов полностью совпадают друг с другом.
Простая линейная регрессия
Простая или одномерная линейная регрессия — это простейший случай линейной регрессии с одной независимой переменной X = ?.
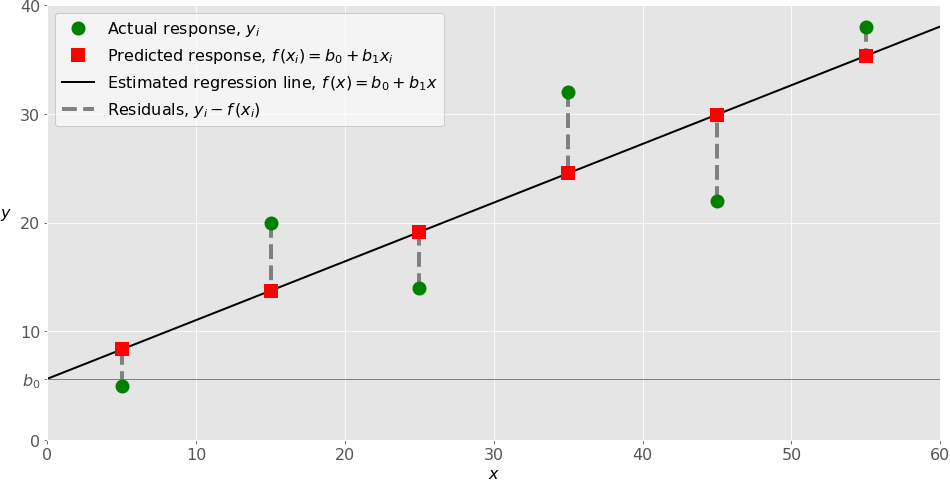
Ниже, на рисунке, показана простая линейная регрессия:
При реализации простой линейной регрессии вы обычно начинаете с заданного набора пар ввода-вывода (x-y) (зеленые кружки). Эти пары — ваши наблюдения. Например, крайнее левое наблюдение (зеленый кружок) имеет вход x = 5, а фактический выход (значение) y = 5. В следующем наблюдении x = 15 и y = 20, и так далее.
Расчетная функция регрессии (черная линия) имеет уравнение f(x) = b_0 + b_1x. Ваша цель — вычислить оптимальные значения прогнозируемых весов b_0, которые минимизируют SSR и определяют предполагаемую функцию регрессии. Значение b_0, также называемое перехватом, показывает точку, в которой линия предполагаемой регрессии пересекает ось. Это значение оценочного ответа f(x) для x = 0. Значение b_1 определяет наклон оцененной линии регрессии.
Прогнозируемые ответы (красные квадраты) — это точки на линии регрессии, которые соответствуют входным значениям. Например, для входа x = 5 прогнозируемый ответ равен f(5) = 8,33 (представлен крайним левым красным квадратом).
Невязки (вертикальные пунктирные серые линии) могут быть вычислены как y_i - f(x_i) = y_i - b_0 - b_1x_i для i = 1,\dots, ?. Это расстояния между зелеными кружками и красными квадратами. Когда вы реализуете линейную регрессию, вы фактически пытаетесь минимизировать эти расстояния и сделать красные квадраты как можно ближе к заранее определенным зеленым кругам.
Множественная линейная регрессия
Множественная или многомерная линейная регрессия — это случай линейной регрессии с двумя или более независимыми переменными. Если есть только две независимые переменные, оценочная функция регрессии будет
f(x_1, x_2) = b_0 + b_1x_1 + b_2x_2.
Он представляет собой плоскость регрессии в трехмерном пространстве. Цель регрессии — определить значения весов b_0, b_1 и b_2 так, чтобы эта плоскость была как можно ближе к реальным значения и дала минимальный SSR. Случай более чем двух независимых переменных аналогичен, но более общий. Предполагаемая функция регрессии —
f(x_1,\dots, x_r) = b_0 + b_1x_1 + \dots + b_rx_r
и необходимо определить r + 1 весовых коэффициентов, когда количество входных данных равно.
Полиномиальная регрессия
Вы можете рассматривать полиномиальную регрессию как обобщенный случай линейной регрессии. Вы предполагаете полиномиальную зависимость между выходом и входами и, следовательно, полиномиальную оценочную функцию регрессии. Другими словами, помимо линейных членов, таких как, ваша функция регрессии f может включать в себя нелинейные члены, такие как b_2x_1^2, b_3x_1^3 или даже b_4x_1x_2, b_5x_1^2x_2 и т. д. Простейший пример полиномиальной регрессии имеет единственную независимую переменную, а предполагаемая функция регрессии — полином степени 2: f(x) = b_0 + b_1x + b_2x^2. Теперь помните, что вы хотите вычислить b_0, b_1 и b_2, которые минимизируют SSR. Это ваши неизвестные! Помня об этом, сравните предыдущую функцию регрессии с функцией f(x_1, x_2) = b_0 + b_1x_1 + b_2x_2, используемой для линейной регрессии. Они выглядят очень похоже и являются линейными функциями от неизвестных b_0, b_1 и b_2. Вот почему вы можете решить задачу полиномиальной регрессии как линейную задачу с членом x^2, рассматриваемым как входная переменная. В случае двух переменных и полинома степени 2 функция регрессии имеет следующий вид:
f(x_1, x_2) = b_0 + b_1x_1 + b_2x_1^2 + b_4x_1x_2 + b_5x_2^2.
Порядок решения проблемы идентичен предыдущему случаю. Вы применяете линейную регрессию для пяти входных данных: x_1, x_2, x_1^2, x_1x_2 и x_2^2. В результате регрессии вы получаете значения шести весов, которые минимизируют SSR: b_0, b_1, b_2, b_3, b_4 и b_5. Конечно, существуют и более общие проблемы, но этого должно быть достаточно, чтобы проиллюстрировать суть дела.
Недостаточное и избыточное соответствие
Один очень важный вопрос, который может возникнуть при реализации полиномиальной регрессии, связан с выбором оптимальной степени функции полиномиальной регрессии. Для этого нет простого рецепта. Это зависит от случая. Тем не менее, вы должны знать о двух проблемах, которые могут возникнуть в результате выбора степени: недостаточное и избыточное соответствие. Неадекватное соответствие возникает, когда модель не может точно уловить зависимости между данными, обычно, из-за ее собственной простоты. Оно часто дает низкий R^2 с известными данными и невозможность обобщения для новых данных. Подгонка происходит, когда модель изучает как зависимости между данными, так и их случайные колебания. Другими словами, модель слишком хорошо изучает существующие данные. Сложные модели, которые имеют множество функций или терминов, часто подвержены переобучению. Применительно к известным данным такие модели обычно дают высокие значения R^2. Однако, они часто плохо обобщаются и имеют значительно меньшее значение R^2 при использовании с новыми данными. Ниже, на рисунке, показаны недостаточно подогнанные, хорошо подогнанные и переобученные (избыточные) модели:

На верхнем левом графике показана линия линейной регрессии с низким значением R^2. Также может быть важно, что прямая линия не может учитывать тот факт, что фактическая реакция увеличивается по мере того, как x перемещается от 25 к нулю. Вероятно, это пример недостаточного соответствия. Верхний правый график иллюстрирует полиномиальную регрессию со степенью, равной 2. В этом случае это может быть оптимальная степень для моделирования этих данных. Модель имеет значение ², которое во многих случаях является удовлетворительным и хорошо показывает тенденции. Нижний левый график представляет полиномиальную регрессию со степенью, равной 3. Значение R^2 выше, чем в предыдущих случаях. Эта модель лучше работает с известными данными, чем предыдущие. Тем не менее, он показывает некоторые признаки переобучения, особенно для входных значений, близких к 60, где линия начинает уменьшаться, хотя фактические данные этого не показывают. Наконец, на правом нижнем графике вы можете увидеть идеальное соответствие: шесть точек и полиномиальная линия степени 5 (или выше) дает R^2 = 1. Каждое фактическое значение равно соответствующему прогнозу. В некоторых ситуациях это может быть именно то, что вы ищете. Однако, во многих случаях это избыточная модель. Вероятно, она будет плохо себя вести с невидимыми данными, особенно, с входными данными, превышающими 50. Например, она предполагает, без каких-либо доказательств, что существует значительное падение для значений > 50 и что y достигает нуля для x около 60. Такое поведение является следствием чрезмерных усилий по изучению и соответствию существующим данным. Существует множество ресурсов, где вы можете найти дополнительную информацию о регрессии в целом и о линейной регрессии в частности. Статьи Регрессионный анализએ и Линейная регрессияએ в Википедии хорошие отправные точки для глубокого изучения.
Реализация линейной регрессии в Python
Пора приступить к реализации линейной регрессии в Python. По сути, все, что вам нужно сделать, это применить подходящие пакеты, их функции и классы.
Пакеты Python для линейной регрессии
Пакет NumPy — это фундаментальный научный пакет Python, который позволяет выполнять множество высокопроизводительных операций с одномерными и многомерными массивами. Он также предлагает множество математических процедур. Конечно, это открытый исходный код. Если вы не знакомы с NumPy, вы можете использовать официальное руководство пользователя NumPy и прочитать Глянь Ма, никаких циклов: работа с массивами, используя NumPy. Кроме того, сравнение производительности в статье Чистый Python против NumPy и TensorFlow. Сравнение производительности может дать вам довольно хорошее представление о приросте производительности, которого вы можете достичь при применении NumPy. Пакет scikit-learn — это широко используемая библиотека Python для машинного обучения, построенная на основе NumPy и некоторые другие пакеты. Они предоставляют инструменты для предварительной обработки данных, уменьшения размерности, реализации регрессии, классификации, кластеризации и многого другого. Как и NumPy, scikit-learn также имеет открытый исходный код. Вы можете проверить страницу Generalized Linear Models на веб-сайте scikit-learn, чтобы узнать больше о линейных моделях и получить более полное представление о том, как работает этот пакет. Если вы хотите реализовать линейную регрессию и вам нужна функциональность, выходящая за рамки scikit-learn, вам следует рассмотреть statsmodels. Это мощный пакет Python для оценки статистических моделей, выполнения тестов и многого другого. Это также открытый исходный код. Вы можете найти дополнительную информацию о статистических моделях на его официальном веб-сайте.
Простая линейная регрессия с помощью scikit-learn
Начнем с простейшего случая, который представляет собой простую линейную регрессию. При реализации линейной регрессии необходимо выполнить пять основных шагов:
- Импортировать необходимые пакеты и классы;
- Предоставить данные для работы и в конечном итоге выполнить соответствующие преобразования;
- Создать модель регрессии и сопоставить его с существующими данными;
- Проверить результаты подгонки модели, чтобы узнать, удовлетворительна ли модель.
Примените модель для прогнозов. Эти шаги являются более или менее общими для большинства регрессионных подходов и реализаций.
Шаг 1. Импорт пакетов и классов
Шаг — импортировать пакет numpy и класс LinearRegression из sklearn.linear_model:
import numpy as np from sklearn.linear_model import LinearRegression
Теперь у вас есть все функции, необходимые для реализации линейной регрессии.
Основным типом данных NumPy является тип массива с именем numpy.ndarray. В остальной части этой статьи термин «массив» используется для обозначения экземпляров типа numpy.ndarray.
Класс sklearn.linear_model.LinearRegression будет использоваться для выполнения линейной и полиномиальной регрессии и соответственно делать прогнозы.
Шаг 2. Предоставьте данные
Второй шаг — определение данных для работы. Входные данные (регрессоры, x) и выходные данные (предиктор, y) должны быть массивами (экземплярами класса numpy.ndarray) или подобными объектами.
Это самый простой способ предоставить данные для регрессии:
x = np.array([5, 15, 25, 35, 45, 55]).reshape((-1, 1)) y = np.array([5, 20, 14, 32, 22, 38])
Теперь у вас есть два массива: входной x и выходной y. Вы должны вызвать .reshape() для x, потому что этот массив должен быть двумерным или, если быть более точным, иметь один столбец и столько строк, сколько необходимо. Именно это и определяет аргумент (-1, 1) функции .reshape().
Вот как теперь выглядят x и y:
>>> print(x) [ [ 5] [15] [25] [35] [45] [55] ] >>> print(y) [ 5 20 14 32 22 38]
Как вы можете видеть, x имеет два измерения, x.shape — это (6, 1), y — одно измерение, а y.shape — (6,).
Шаг 3. Создайте модель и подгоните ее
Следующим шагом является создание модели линейной регрессии и ее аппроксимация с использованием существующих данных.
Давайте создадим экземпляр класса LinearRegression, который будет представлять регрессионную модель:
model = LinearRegression()
Этот оператор создает переменную модель как экземпляр LinearRegression. Вы можете предоставить LinearRegression несколько дополнительных параметров:
- fit_intercept — это логическое значение (по умолчанию
True), которое определяет, следует ли вычислять точку пересечения b_0 (True) или считать ее равной нулю (False). - normalize — это логическое значение (по умолчанию
False), которое определяет, следует ли нормализовать входные переменные (True) или нет (False). - copy_X — это логическое значение (по умолчанию
True), которое решает, копировать (True) или перезаписывать входные переменные (False). - n_jobs является целым числом или
None(по умолчанию) и представляет количество заданий, используемых в параллельных вычислениях.Noneобычно означает одно задание, а-1— использовать все процессоры. В этом примере используются значения по умолчанию для всех параметров.
Пришло время начать пользоваться моделью. Во-первых, вам нужно вызвать .fit() для модели:
model.fit(x, y)
С помощью .fit() вы вычисляете оптимальные значения весов b_0 и b_1, используя существующие входные и выходные данные (x и y) в качестве аргументов. Другими словами, .fit() соответствует модели. Он возвращает self, которое является самой переменной моделью. Вот почему вы можете заменить последние два утверждения на это:
model = LinearRegression().fit(x, y)
Шаг 4. Получите результаты
После того, как вы настроили свою модель, вы можете получить результаты, чтобы проверить, удовлетворительно ли она работает и интерпретировать ее.
Вы можете получить коэффициент детерминации (?^2) с помощью .score(), вызванного для модели:
>>> r_sq = model.score(x, y)
>>> print('coefficient of determination:', r_sq)
coefficient of determination: 0.715875613747954
Когда вы применяете .score(), аргументы также являются предиктором x и регрессором y, а возвращаемое значение — ?^2.
Атрибуты модели: .intercept_, который представляет коэффициент, и .coef_, который представляет b_1:
>>> print('intercept:', model.intercept_)
intercept: 5.633333333333329
>>> print('slope:', model.coef_)
slope: [0.54]
В приведенном выше коде показано, как получить b_0 и b_1. Вы можете заметить, что .intercept_ — это скаляр, а .coef_ — это массив.
Значение b_0 = 5,63 (приблизительно) показывает, что ваша модель предсказывает реакцию 5,63, когда x равно нулю. Значение b_1 = 0,54 означает, что прогнозируемый ответ увеличивается на 0,54, когда x увеличивается на единицу.
Вы должны заметить, что вы также можете предоставить y как двумерный массив. В этом случае вы получите аналогичный результат. Вот как это может выглядеть:
>>> new_model = LinearRegression().fit(x, y.reshape((-1, 1)))
>>> print('intercept:', new_model.intercept_)
intercept: [5.63333333]
>>> print('slope:', new_model.coef_)
slope: [ [0.54] ]
Как видите, этот пример очень похож на предыдущий, но в данном случае .intercept_ — это одномерный массив с единственным элементом b_0, а .coef_ — это двумерный массив с единственным элементом b_1.
Шаг 5. Спрогнозируйте ответ
Как только будет создана удовлетворительная модель, вы можете использовать ее для прогнозов с использованием существующих или новых данных.
Чтобы получить прогнозируемый ответ, используйте .predict():
>>> y_pred = model.predict(x)
>>> print('predicted response:', y_pred, sep='\n')
predicted response:
[ 8.33333333 13.73333333 19.13333333 24.53333333 29.93333333 35.33333333]
При применении .predict() вы передаете регрессор в качестве аргумента и получаете соответствующий прогнозируемый ответ.
Это почти идентичный способ предсказать ответ:
>>> y_pred = model.intercept_ + model.coef_ * x
>>> print('predicted response:', y_pred, sep='\n')
predicted response:
[ [ 8.33333333]
[13.73333333]
[19.13333333]
[24.53333333]
[29.93333333]
[35.33333333] ]
В этом случае вы умножаете каждый элемент x на model.coef_ и добавляете model.intercept_ к продукту.
Вывод здесь отличается от предыдущего примера только размерами. Прогнозируемый ответ теперь представляет собой двумерный массив, тогда как в предыдущем случае он имел одно измерение.
Если вы уменьшите количество измерений x до одного, эти два подхода дадут одинаковый результат. Вы можете сделать это, заменив x на x.reshape(-1), x.flatten() или x.ravel() при умножении на model.coef_.
На практике для прогнозов часто применяются регрессионные модели. Это означает, что вы можете использовать подогнанные модели для расчета результатов на основе некоторых других, новых входных данных:
>>> x_new = np.arange(5).reshape((-1, 1)) >>> print(x_new) [ [0] [1] [2] [3] [4] ] >>> y_new = model.predict(x_new) >>> print(y_new) [5.63333333 6.17333333 6.71333333 7.25333333 7.79333333]
Здесь .predict() применяется к новому регрессору x_new и дает ответ y_new. В этом примере удобно использовать arange() из numpy для создания массива с элементами от 0 (включительно) до 5 (исключая), то есть 0, 1, 2, 3 и 4.
Вы можете найти дополнительную информацию о LinearRegression на официальной странице документации.
Множественная линейная регрессия с помощью scikit-learn
Вы можете реализовать множественную линейную регрессию, выполнив те же шаги, что и для простой регрессии.
Шаги 1 и 2: Импорт пакетов и классов и предоставление данных
Сначала вы импортируете numpy и sklearn.linear_model.LinearRegression и предоставляете известные входные и выходные данные:
import numpy as np from sklearn.linear_model import LinearRegression x = [ [0, 1], [5, 1], [15, 2], [25, 5], [35, 11], [45, 15], [55, 34], [60, 35] ] y = [4, 5, 20, 14, 32, 22, 38, 43] x, y = np.array(x), np.array(y)
Это простой способ определить вход x и выход y. Вы можете распечатать x и y, чтобы увидеть, как они выглядят сейчас:
>>> print(x) [ [ 0 1] [ 5 1] [15 2] [25 5] [35 11] [45 15] [55 34] [60 35] ] >>> print(y) [ 4 5 20 14 32 22 38 43]
В множественной линейной регрессии x — это двумерный массив, по крайней мере, с двумя столбцами, а y — обычно одномерный массив. Это простой пример множественной линейной регрессии и x имеет ровно два столбца.
Шаг 3: Создайте модель и подгоните ее
Следующим шагом будет создание модели регрессии как экземпляр LinearRegression и подгонка ее с помощью .fit():
model = LinearRegression().fit(x, y)
Результатом этого оператора является переменная модель, ссылающаяся на объект типа LinearRegression. Он представляет собой регрессионную модель, оснащенную существующими данными.
Шаг 4: Получение результатов
Вы можете получить свойства модели так же, как и в случае простой линейной регрессии:
>>> r_sq = model.score(x, y)
>>> print('coefficient of determination:', r_sq)
coefficient of determination: 0.8615939258756776
>>> print('intercept:', model.intercept_)
intercept: 5.52257927519819
>>> print('slope:', model.coef_)
slope: [0.44706965 0.25502548]
Вы получаете значение R^2 с помощью .score() и значения оценщиков коэффициентов регрессии с .intercept_ и .coef_. Опять же, .intercept_ содержит смещение b_0, в то время как теперь .coef_ — это массив, содержащий b_1 и b_2 соответственно. В этом примере перехват составляет приблизительно 5,52, и это значение прогнозируемого отклика, когда x_1 = x_2 = 0. Увеличение из x_1 на 1 дает рост прогнозируемой реакции на 0,45. Точно так же, когда x_1 увеличивается на 1, отклик увеличивается на 0,26.
Шаг 5: Прогнозирование отклика
Прогнозы также работают так же, как и в случае простой линейной регрессии:
>>> y_pred = model.predict(x)
>>> print('predicted response:', y_pred, sep='\n')
predicted response:
[ 5.77760476 8.012953 12.73867497 17.9744479 23.97529728 29.4660957
38.78227633 41.27265006]
Прогнозируемый ответ получается с помощью .predict(), который очень похож на следующий:
>>> y_pred = model.intercept_ + np.sum(model.coef_ * x, axis=1)
>>> print('predicted response:', y_pred, sep='\n')
predicted response:
[ 5.77760476 8.012953 12.73867497 17.9744479 23.97529728 29.4660957
38.78227633 41.27265006]
Вы можете предсказать выходные значения, умножив каждый столбец ввода на соответствующий вес, суммируя результаты и добавляя точку пересечения к сумме. Вы также можете применить эту модель к новым данным:
>>> x_new = np.arange(10).reshape((-1, 2)) >>> print(x_new) [ [0 1] [2 3] [4 5] [6 7] [8 9] ] >>> y_new = model.predict(x_new) >>> print(y_new) [ 5.77760476 7.18179502 8.58598528 9.99017554 11.3943658 ]
Это прогноз с использованием модели линейной регрессии.
Полиномиальная регрессия с помощью scikit-learn
Реализация полиномиальной регрессии с помощью scikit-learn очень похожа на линейную регрессию. Есть только один дополнительный шаг: вам нужно преобразовать массив входных данных, чтобы включить нелинейные термины, такие как x^2.
Шаг 1: Импортировать пакеты и классы
Помимо numpy и sklearn.linear_model.LinearRegression, вы также должны импортировать класс PolynomialFeatures из sklearn.preprocessing:
import numpy as np from sklearn.linear_model import LinearRegression from sklearn.preprocessing import PolynomialFeatures
Импорт завершен, и у вас есть все необходимое для работы.
Шаг 2а: предоставьте данные
Этот шаг определяет ввод и вывод и такой же, как и в случае линейной регрессии:
x = np.array([5, 15, 25, 35, 45, 55]).reshape((-1, 1)) y = np.array([15, 11, 2, 8, 25, 32])
Это новый шаг, который необходимо реализовать для полиномиальной регрессии!
Как вы видели ранее, вам необходимо включить x^2 (и, возможно, другие термины) в качестве дополнительных функций при реализации полиномиальной регрессии. По этой причине, вы должны преобразовать входной массив x, чтобы он содержал дополнительный столбец (столбцы) со значениями x^2 (и, в конечном итоге, другими функциями).
Можно преобразовать входной массив несколькими способами (например, с помощью insert() из numpy), но класс PolynomialFeatures очень удобен для этой цели. Давайте создадим экземпляр этого класса:
transformer = PolynomialFeatures(degree=2, include_bias=False)
Преобразователь переменных относится к экземпляру PolynomialFeatures, который вы можете использовать для преобразования входного x.
Вы можете указать несколько дополнительных параметров для PolynomialFeatures:
- degree — это целое число (по умолчанию 2), представляющее степень функции полиномиальной регрессии.
- Interaction_only — это логическое значение (по умолчанию
False), которое определяет, следует ли включать только функции взаимодействия(True) или все функции (False). - include_bias — это логическое значение (по умолчанию
True), которое решает, включать ли столбец смещения (перехвата) единиц (True) или нет (False).
В этом примере используются значения по умолчанию для всех параметров, но иногда вы захотите поэкспериментировать со степенью функции, и в любом случае может быть полезно привести этот аргумент.
Перед применением transformer его нужно подогнать с помощью .fit():
transformer.fit(x)
После установки code>transformer он готов к созданию нового измененного входа. Для этого вы применяете .transform():
x_ = transformer.transform(x)
Это преобразование входного массива с помощью .transform(). Он принимает входной массив в качестве аргумента и возвращает измененный массив.
Вы также можете использовать .fit_transform() для замены трех предыдущих операторов только одним:
x_ = PolynomialFeatures(degree=2, include_bias=False).fit_transform(x)
Это подгонка и преобразование входного массива в один оператор с помощью .fit_transform(). Он также принимает входной массив и фактически делает то же самое, что .fit() и .transform(), вызываемые в этом порядке. Он также возвращает измененный массив. Так выглядит новый входной массив:
>>> print(x_) [ [ 5. 25.] [ 15. 225.] [ 25. 625.] [ 35. 1225.] [ 45. 2025.] [ 55. 3025.] ]
Модифицированный входной массив содержит два столбца: один с исходными входами, а другой с их квадратами.
Вы можете найти дополнительную информацию о PolynomialFeatures на официальной странице документации.
Шаг 3. Создайте модель и подгоните её
Этот шаг также такой же, как и в случае линейной регрессии. Вы создаете и подгоняете модель:
model = LinearRegression().fit(x_, y)
Теперь регрессионная модель создана и настроена. Готова к применению.
Вы должны помнить, что первый аргумент .fit() — это модифицированный входной массив x_, а не исходный x.
Шаг 4. Получите результаты
Получить свойства модели можно так же, как и в случае линейной регрессии:
>>> r_sq = model.score(x_, y)
>>> print('coefficient of determination:', r_sq)
coefficient of determination: 0.8908516262498564
>>> print('intercept:', model.intercept_)
intercept: 21.372321428571425
>>> print('coefficients:', model.coef_)
coefficients: [-1.32357143 0.02839286]
Опять же, .score() возвращает R^2. Его первым аргументом также является измененный вход x_, а не x. Значения весов связаны с .intercept_ и .coef_: .intercept_ представляет b_0, а .coef_ ссылается на массив, содержащий b_1 и b_2 соответственно.
Вы можете получить очень похожий результат с разными аргументами преобразования и регрессии:
x_ = PolynomialFeatures(degree=2, include_bias=True).fit_transform(x)
Если вы вызываете PolynomialFeatures с параметром по умолчанию include_bias = True (или просто опускаете его), вы получите новый входной массив x_ с дополнительным крайним левым столбцом, содержащим только единицы. Этот столбец соответствует перехвату. Вот как в этом случае выглядит модифицированный входной массив:
>>> print(x_) [ [1.000e+00 5.000e+00 2.500e+01] [1.000e+00 1.500e+01 2.250e+02] [1.000e+00 2.500e+01 6.250e+02] [1.000e+00 3.500e+01 1.225e+03] [1.000e+00 4.500e+01 2.025e+03] [1.000e+00 5.500e+01 3.025e+03] ]
Первый столбец x_ содержит единицы, второй — значения x, а третий — квадраты x.
Перехват уже включен в крайний левый столбец единиц, и вам не нужно включать его снова при создании экземпляра LinearRegression. Таким образом, вы можете указать fit_intercept = False. Вот так выглядит следующее утверждение:
>>> print(x_) model = LinearRegression(fit_intercept=False).fit(x_, y)
Переменная model снова соответствует новому входному массиву x_. Следовательно, x_ следует передавать в качестве первого аргумента вместо x.
Этот подход дает следующие результаты, аналогичные предыдущему:
>>> print(x_)
>>> r_sq = model.score(x_, y)
>>> print('coefficient of determination:', r_sq)
coefficient of determination: 0.8908516262498565
>>> print('intercept:', model.intercept_)
intercept: 0.0
>>> print('coefficients:', model.coef_)
coefficients: [21.37232143 -1.32357143 0.02839286]
Вы видите, что теперь .intercept_ равен нулю, но .coef_ фактически содержит b_0 в качестве своего первого элемента. В остальном все то же самое.
Шаг 5. Спрогнозируйте ответ
Если вы хотите получить предсказанный ответ, просто используйте .predict(), но помните, что аргументом должен быть измененный вход x_ вместо старого x:
>>> y_pred = model.predict(x_)
>>> print('predicted response:', y_pred, sep='\n')
predicted response:
[15.46428571 7.90714286 6.02857143 9.82857143 19.30714286 34.46428571]
Как видите, прогноз работает почти так же, как и в случае линейной регрессии. Просто требуется модифицированный ввод вместо оригинала.
Вы можете применить идентичную процедуру, если у вас есть несколько входных переменных. У вас будет входной массив с более чем одним столбцом, но все остальное останется прежним. Вот пример:
# Step 1: Import packages import numpy as np from sklearn.linear_model import LinearRegression from sklearn.preprocessing import PolynomialFeatures # Step 2a: Provide data x = [ [0, 1], [5, 1], [15, 2], [25, 5], [35, 11], [45, 15], [55, 34], [60, 35] ] y = [4, 5, 20, 14, 32, 22, 38, 43] x, y = np.array(x), np.array(y) # Step 2b: Transform input data x_ = PolynomialFeatures(degree=2, include_bias=False).fit_transform(x) # Step 3: Create a model and fit it model = LinearRegression().fit(x_, y) # Step 4: Get results r_sq = model.score(x_, y) intercept, coefficients = model.intercept_, model.coef_ # Step 5: Predict y_pred = model.predict(x_)
Этот пример регрессии дает следующие результаты и прогнозы:
>>> print('coefficient of determination:', r_sq)
coefficient of determination: 0.9453701449127822
>>> print('intercept:', intercept)
intercept: 0.8430556452395734
>>> print('coefficients:', coefficients, sep='\n')
coefficients:
[ 2.44828275 0.16160353 -0.15259677 0.47928683 -0.4641851 ]
>>> print('predicted response:', y_pred, sep='\n')
predicted response:
[ 0.54047408 11.36340283 16.07809622 15.79139 29.73858619 23.50834636
39.05631386 41.92339046]
В этом случае имеется шесть коэффициентов регрессии (включая точку пересечения), как показано в оценочной функции регрессии
f(x_1, x_2) = b_0 + b_1x_1 + b_2x_2 + b_3x_1^2 + b_4x_1x_2 + b_5x_2^2.
Вы также можете заметить, что полиномиальная регрессия дала более высокий коэффициент детерминации, чем множественная линейная регрессия для той же проблемы.
Сначала можно было подумать, что получение такой большой площади — отличный результат, что может быть.
Однако в реальных ситуациях наличие сложной модели и R^2, очень близкого к 1, также может быть признаком переобучения. Чтобы проверить производительность модели, вы должны протестировать ее с новыми данными, то есть с наблюдениями, которые не используются для соответствия (обучения) модели.
Чтобы узнать, как разделить набор данных на обучающие и тестовые подмножества, ознакомьтесь с Split Your Dataset With scikit-learn’s train_test_split().
Расширенная линейная регрессия с моделями статистики
Вы можете относительно легко реализовать линейную регрессию в Python, используя также пакет statsmodels. Обычно это желательно, когда есть потребность в более подробных результатах.
Процедура аналогична scikit-learn.
Шаг 1. Импортируйте пакеты
Сначала вам нужно сделать импорт. В дополнение к numpy вам необходимо импортировать statsmodels.api:
import numpy as np import statsmodels.api as sm
Теперь у вас есть нужные пакеты.
Шаг 2. Предоставьте данные и преобразуйте входные данные
Вы можете предоставить входные и выходные данные так же, как и при использовании scikit-learn:
x = [ [0, 1], [5, 1], [15, 2], [25, 5], [35, 11], [45, 15], [55, 34], [60, 35] ] y = [4, 5, 20, 14, 32, 22, 38, 43] x, y = np.array(x), np.array(y)
Массивы ввода и вывода созданы, но работа еще не сделана.
Вам нужно добавить столбец единиц к входным данным, если вы хотите, чтобы statsmodels вычисляла точку пересечения b_0. По умолчанию b_0 не учитывается. Это всего лишь вызов одной функции:
x = sm.add_constant(x)
Вот как вы добавляете столбец единиц к x с помощью add_constant(). Он принимает входной массив x в качестве аргумента и возвращает новый массив со столбцом единиц, вставленных в начало. Вот как теперь выглядят x и y:
>>> print(x) [ [ 1. 0. 1.] [ 1. 5. 1.] [ 1. 15. 2.] [ 1. 25. 5.] [ 1. 35. 11.] [ 1. 45. 15.] [ 1. 55. 34.] [ 1. 60. 35.] ] >>> print(y) [ 4 5 20 14 32 22 38 43]
Вы можете видеть, что измененный x имеет три столбца: первый столбец из единиц (соответствующий b_0 и заменяющий точку пересечения), а также два столбца исходных объектов.
Шаг 3. Создайте модель и подгоните ее
Модель регрессии, основанная на обычных методах наименьших квадратов, является экземпляром класса statsmodels.regression.linear_model.OLS. Вот как вы можете её получить:
model = sm.OLS(y, x)
Здесь нужно быть осторожным! Обратите внимание, что первый аргумент — это вывод, за которым следует ввод. Есть еще несколько необязательных параметров.
Чтобы найти дополнительную информацию об этом классе, посетите официальную страницу документации.
Как только ваша модель создана, вы можете применить к ней .fit():
results = model.fit()
Вызывая .fit(), вы получаете переменную results, которая является экземпляром класса statsmodels.regression.linear_model.RegressionResultsWrapper. Этот объект содержит много информации о регрессионной модели.
Шаг 4. Получите результаты
Переменная results относится к объекту, который содержит подробную информацию о результатах линейной регрессии. Объяснение их выходит далеко за рамки этой статьи, но здесь вы узнаете, как их извлечь.
Вы можете вызвать .summary(), чтобы получить таблицу с результатами линейной регрессии:
>>> print(results.summary()) OLS Regression Results ============================================================================== Dep. Variable: y R-squared: 0.862 Model: OLS Adj. R-squared: 0.806 Method: Least Squares F-statistic: 15.56 Date: Sun, 17 Feb 2019 Prob (F-statistic): 0.00713 Time: 19:15:07 Log-Likelihood: -24.316 No. Observations: 8 AIC: 54.63 Df Residuals: 5 BIC: 54.87 Df Model: 2 Covariance Type: nonrobust ============================================================================== coef std err t P>|t| [0.025 0.975] ------------------------------------------------------------------------------ const 5.5226 4.431 1.246 0.268 -5.867 16.912 x1 0.4471 0.285 1.567 0.178 -0.286 1.180 x2 0.2550 0.453 0.563 0.598 -0.910 1.420 ============================================================================== Omnibus: 0.561 Durbin-Watson: 3.268 Prob(Omnibus): 0.755 Jarque-Bera (JB): 0.534 Skew: 0.380 Prob(JB): 0.766 Kurtosis: 1.987 Cond. No. 80.1 ============================================================================== Warnings: [1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
Эта таблица очень обширна. Вы можете найти множество статистических значений, связанных с линейной регрессией, включая R^2, b_0, b_1 и b_2.
В этом конкретном случае вы можете получить предупреждение, связанное с эксцессом. Это связано с небольшим количеством предоставленных наблюдений.
Вы можете извлечь любое из значений таблицы выше. Например:
>>> print('coefficient of determination:', results.rsquared)
coefficient of determination: 0.8615939258756777
>>> print('adjusted coefficient of determination:', results.rsquared_adj)
adjusted coefficient of determination: 0.8062314962259488
>>> print('regression coefficients:', results.params)
regression coefficients: [5.52257928 0.44706965 0.25502548]
Вот как можно получить некоторые результаты линейной регрессии:
- .rsquared содержит R^2.
- .rsquared_adj представляет собой скорректированный R^2 (R^2 скорректированный согласно количеству входных функций).
- .params ссылается на массив с помощью b_0, b_1 и b_2 соответственно.
Вы также можете заметить, что эти результаты идентичны результатам, полученным с помощью scikit-learn решать ту же проблему.
Для получения дополнительной информации о результатах линейной регрессии посетите официальную страницу документации.
Шаг 5. Спрогнозируйте ответ
Вы можете получить прогнозируемый ответ на входные значения, используемые для создания модели, используя .fittedvalues или .predict() с входным массивом в качестве аргумента:
>>> print('predicted response:', results.fittedvalues, sep='\n')
predicted response:
[ 5.77760476 8.012953 12.73867497 17.9744479 23.97529728 29.4660957
38.78227633 41.27265006]
>>> print('predicted response:', results.predict(x), sep='\n')
predicted response:
[ 5.77760476 8.012953 12.73867497 17.9744479 23.97529728 29.4660957
38.78227633 41.27265006]
Это прогнозируемый ответ для известных входов. Если вам нужны прогнозы с новыми регрессорами, вы также можете применить .predict() с новыми данными в качестве аргумента:
>>> x_new = sm.add_constant(np.arange(10).reshape((-1, 2))) >>> print(x_new) [ [1. 0. 1.] [1. 2. 3.] [1. 4. 5.] [1. 6. 7.] [1. 8. 9.] ] >>> y_new = results.predict(x_new) >>> print(y_new) [ 5.77760476 7.18179502 8.58598528 9.99017554 11.3943658 ]
Вы можете заметить, что прогнозируемые результаты такие же, как и полученные с помощью scikit-learn для той же проблемы.
За пределами линейной регрессии
Линейная регрессия иногда не подходит, особенно для нелинейных моделей высокой сложности.
К счастью, есть и другие методы регрессии, подходящие для случаев, когда линейная регрессия не работает. Некоторые из них — вспомогательные векторные машины, деревья решений, случайный лес и нейронные сети.
Существует множество библиотек Python для регрессии с использованием этих методов. Большинство из них бесплатны и имеют открытый исходный код. Это одна из причин, почему Python является одним из основных языков программирования для машинного обучения.
Пакет scikit-learn предоставляет средства для использования других техник регрессии очень похожим образом на то, что вы видели. Он содержит классы для опорных векторных машин, деревьев решений, случайного леса и т.д. С методами .fit(), .predict(), .score() и т.д.
Заключение
Теперь вы знаете, что такое линейная регрессия и как ее можно реализовать с помощью Python и трех пакетов с открытым исходным кодом: NumPy, scikit-learn и statsmodels.
Вы используете NumPy для обработки массивов.
Линейная регрессия реализуется следующим образом:
- scikit-learn, не нужны ли вам подробные результаты и вы хотите использовать подход, совместимый с другими методами регрессии
- statsmodels, если вам нужны расширенные статистические параметры модели
Оба подхода стоит изучить, как использовать, и изучить их дальше. Ссылки в этой статье могут быть очень полезны для этого.При выполнении линейной регрессии в Python вы можете выполнить следующие действия:
- Импортируйте нужные вам пакеты и классы.
- Предоставлять данные для работы и в конечном итоге выполнять соответствующие преобразования.
- Создайте регрессионную модель и сопоставьте ее с существующими данными.
- Проверьте результаты подгонки модели, чтобы узнать, удовлетворительна ли модель.
- Примените модель для прогнозов.
Если у вас есть вопросы или комментарии, пожалуйста, оставьте их в разделе комментариев ниже.
По мотивам Linear Regression in Python